练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

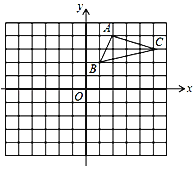
    【题目】如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，4），请解答下列问题：

    （1）画出△ABC关于x轴对称的△A1B1C1（点A的对应点为A1，点B的对应点为B1，点C的对应点为C1），并写出点A1的坐标；

    （2）画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2（点A1的对应点为A2，点B1的对应点为B2，点C1的对应点为C2）．

    【答案】（1）见解析，A1（2，-4）；（2）见解析

    【解析】

    （1）分别作出A，B，C的对应点A1，B1，C1，根据轴对称的性质得出A1的坐标；

    （2）分别作出点A1，B1，C1的对应点A2，B2，C2即可．

    解：（1）△ABC关于x轴对称的△A1B1C1如图所示，

    ∵A（2，4），

    ∴A1（2，-4）；

    （2）△A2B2C2即为所求．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某公司共有三个部门，根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图．

    各部门人数及每人所创年利润统计表

    部门

    员工人数

    每人所创的年利润/万元

    A

    5

    10

    B

    8

    C

    5

    （1）①在扇形图中，C部门所对应的圆心角的度数为___________；

    ②在统计表中，___________，___________；

    （2）求这个公司平均每人所创年利润．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，以矩形ABCD的边CD为直径作⊙O，点E是AB 的中点，连接CE交⊙O于点F，连接AF并延长交BC于点H．

    （1）若连接AO，试判断四边形AECO的形状，并说明理由；

    （2）求证：AH是⊙O的切线；

    （3）若AB＝6，CH＝2，则AH的长为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC为⊙O的内接三角形，BC=24 , ,点D为弧BC上一动点，CE垂直直线OD于点E, 当点D由B点沿弧BC运动到点C时，点E经过的路径长为（ ）

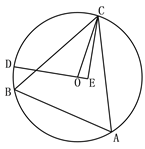
    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形中，，点为对称中心，过点的直线交于点，交于点．

    (1)求证： ；

    (2)当时，求线段的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

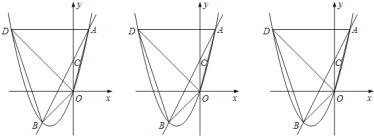
    【题目】如图，二次函数y＝ax2+bx（a≠0）的图象经过点A（1，4），对称轴是直线x＝﹣，线段AD平行于x轴，交抛物线于点D，在y轴上取一点C（0，2），直线AC交抛物线于点B，连结OA，OB，OD，BD．

    （1）求该二次函数的解析式；

    （2）设点F是BD的中点，点P是线段DO上的动点，将△BPF沿边PF翻折，得到△B′PF，使△B′PF与△DPF重叠部分的面积是△BDP的面积的，若点B′在OD上方，求线段PD的长度；

    （3）在（2）的条件下，过B′作B′H⊥PF于H，点Q在OD下方的抛物线上，连接AQ与B′H交于点M，点G在线段AM上，使∠HPN+∠DAQ＝135°，延长PG交AD于N．若AN+B′M＝，求点Q的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为深化“携手节能低碳，共建碧水蓝天”活动，发展“低碳经济”，某单位进行技术革新，让可再生资源重新利用．今年1月份，再生资源处理量为40吨，从今年1月1日起，该单位每月再生资源处理量每一个月将提高10吨．月处理成本（元）与月份（月）之间的关系可近似地表示为：，每处理一吨再生资源得到的新产品的售价定为100元．若该单位每月再生资源处理量为（吨），每月的利润为（元）．

    （1）分别求出与，与的函数关系式；

    （2）在今年内该单位哪个月获得利润达到5800元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，，．点从点出发，以每秒个单位长度的速度沿向点运动，过点作交边或边于点，点是射线上的一点，且，以、为邻边作矩形．设矩形与重叠部分图形的面积为，点的运动时间为（秒）．

    （1）用含的代数式表示线段的长．

    （2）当点落在上时，求的值．

    （3）当矩形与重叠部分图形为四边形时，求与之间的函数关系式．

    （4）点与点同时出发，在线段上以每秒2个单位长度的速度沿往返运动，连结、，当点停止时点也随之停止，直接写出矩形面积是面积的4倍时的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点A（－5，0），以OA为半径作半圆，点C是第一象限内圆周上一动点，连结AC、BC，并延长BC至点D，使CD＝BC，过点D作x轴垂线，分别交x轴、直线AC于点E、F，点E为垂足，连结OF．

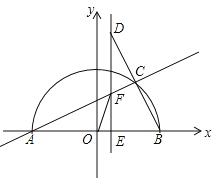
    （1）当∠BAC＝30时，求△ABC的面积；

    （2）当DE＝8时，求线段EF的长；

    （3）在点C运动过程中，是否存在以点E、O、F为顶点的三角形与△ABC相似，若存在，请求出点E的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案