
【题目】已知:如图,Rt△ABC中,∠C=90°,∠BAC=30°,延长CA至D点,使AD=AB.求:
(1)求∠D及∠DBC;
(2)求tanD及tan∠DBC;
(3)请用类似的方法,求tan22.5°.
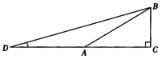
【答案】(1)∠D=15°,∠DBC=75°;(2)![]() ;
;![]() (3)
(3)![]()
【解析】
(1)利用外角性质得∠D=15°,∠DBC=75°;(2)设BC=1,根据30°角所对直角边等于斜边一半表示出直角边,利用正切值定义即可解题;(3)作出图形,根据外角性质和等腰直角三角形性质即可解题,见详解.
解:(1) ∵AD=AB
∴ ∠D+∠DBA=30°(外角性质)
∴∠D=15°,∠DBC=15°+60°=75°;
(2)设BC=1 则AB=AD=2,(30°角所对直角边等于斜边一半)
∴AC=![]() (勾股定理)
(勾股定理)
∴![]()
![]() ,
,
(3)见下图, Rt△ABC中,∠C=90°,∠BAC=45°,延长CA至D点,使AD=AB.
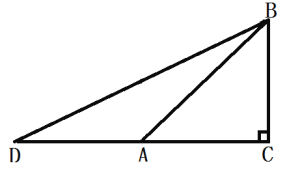
∴ ∠D+∠DBA=45°(外角性质)
∴∠D=22.5°,
设BC=1,
∴AC=1,AB=![]() ,
,
∴![]()


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
【题目】一个盒中有4个完全相同的小球,把它们分别标号为1,2,3,4,随机摸取一个小球然后放回,再随机摸出一个小球.
(Ⅰ)请用列表法(或画树状图法)列出所有可能的结果;
(Ⅱ)求两次取出的小球标号相同的概率;
(Ⅲ)求两次取出的小球标号的和大于6的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图,则一次函数y=bx+b2﹣4ac与反比例函数y=![]() 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
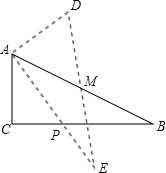
【题目】如图,在△ABC中,∠C=90°,AB=10,cosB=![]() ,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是__________.
,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=x+2与双曲线![]() 相交于点A(m,3).
相交于点A(m,3).
(1)求反比例函数的表达式;
(2)画出直线和双曲线的示意图;
(3)若P是坐标轴上一点,当OA=PA时.直接写出点P的坐标.
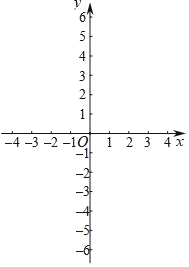
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一次函数y=kx+b与反比例函数y=![]() 的图象如图所示,则关于x的不等式kx+b﹣
的图象如图所示,则关于x的不等式kx+b﹣![]() ≤﹣2的解集为( )
≤﹣2的解集为( )
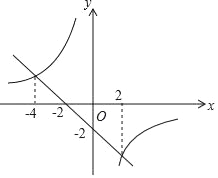
A. 0<x≤2或x≤﹣4 B. ﹣4≤x<0或x≥2
C. ![]() ≤x<0或x
≤x<0或x![]() D. x
D. x![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件30元,售价为每件40元,每周可卖出180件;如果每件商品的售价每上涨1元,则每周就会少卖出5件,但每件售价不能高于50元,设每件商品的售价上涨x元(x为整数),每周的销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)每件商品的售价为多少元时,每周可获得最大利润?最大利润是多少?
(3)每件商品的售价定为多少元时,每周的利润恰好是2145元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为线段AB的中点,AB=4cm,P1、P2、P3、P4到点O的距离分别是1cm、2cm、2.8cm、1.7cm,下列四点中能与A、B构成直角三角形的顶点是( )
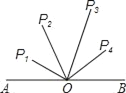
A. P1 B. P2 C. P3 D. P4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com