
【题目】在平面直角坐标系xOy中,直线y=x+2与双曲线![]() 相交于点A(m,3).
相交于点A(m,3).
(1)求反比例函数的表达式;
(2)画出直线和双曲线的示意图;
(3)若P是坐标轴上一点,当OA=PA时.直接写出点P的坐标.
【答案】(1)y=![]() ;(2)见解析;(3) P(0,6)或P(2,0)
;(2)见解析;(3) P(0,6)或P(2,0)
【解析】
(1)利用待定系数法即可求出反比例函数的表达式;
(2)利用描点法画出函数图象即可;
(3)当点P在y轴上,过点A作AE⊥PO,可求出P的坐标(0,6);当点P在x轴上,过点A作AF⊥PO,则OF=1,可得P的坐标(2,0).
解:(1)∵直线y=x+2与双曲线![]() 相交于点A(m,3).
相交于点A(m,3).
∴3=m+2,
∴m=1.
∴A(1,3)
把A(1,3)代入![]()
∴k=3×1=3,
∴![]() .
.
(2)直线和双曲线的示意图如图所示:
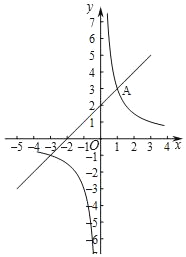
(3)当点P在y轴上,过点A作AE⊥PO,则OE=3,
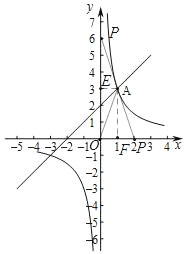
∵OA=PA,AE⊥PO,
∴PE=OE=3,
∴OP=6,
∴点P的坐标为(0,6)
若点P在x轴上,过点A作AF⊥PO,则OF=1
∵OA=PA,AF⊥PO,
∴OF=PF=1,
∴OP=2
∴点P坐标为(2,0)
综上所述,P(0,6)或P(2,0)


科目:初中数学 来源: 题型:
【题目】如图,将△OAB绕O点逆时针旋转60°得到△OCD,若OA=4,∠AOB=35°,则下列结论错误的是( )
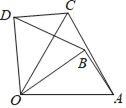
A. ∠BDO=60° B. ∠BOC=25° C. OC=4 D. BD=4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“书香八桂,阅读圆梦”读书活动中,某中学设置了书法、国学诵读、演讲、征文四个比赛项目(每人只参加一个项目),九(2)班全班同学都参加了比赛,该班班长为了了解本班同学参加各项比赛的情况,收集整理数据后,绘制以下不完整的折线统计图(图1)和扇形统计图(图2),根据图表中的信息解答下列各题:
(1)请求出九(2)全班人数;
(2)请把折线统计图补充完整;
(3)南南和宁宁参加了比赛,请用“列表法”或“画树状图法”求出他们参加的比赛项目相同的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
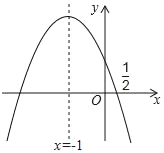
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1,且过点(![]() ,0).有下列结论:①abc>0;②25a﹣10b+4c=0;③a﹣2b+4c=0;④a﹣b≥m(am﹣b);⑤3b+2c>0;其中所有正确的结论是_____(填写正确结论的序号).
,0).有下列结论:①abc>0;②25a﹣10b+4c=0;③a﹣2b+4c=0;④a﹣b≥m(am﹣b);⑤3b+2c>0;其中所有正确的结论是_____(填写正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
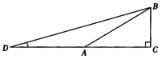
【题目】已知:如图,Rt△ABC中,∠C=90°,∠BAC=30°,延长CA至D点,使AD=AB.求:
(1)求∠D及∠DBC;
(2)求tanD及tan∠DBC;
(3)请用类似的方法,求tan22.5°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(x,0),B(x,y),若线段AB上存在一点Q满足![]() ,则称点Q是线段AB的“倍分点”.
,则称点Q是线段AB的“倍分点”.
(1)若点A(1,0),AB=3,点Q是线段AB的“倍分点”.
①求点Q的坐标;
②若点A关于直线y=x的对称点为A′,当点B在第一象限时,求![]() ;
;
(2)⊙T的圆心T(0,t),半径为2,点Q在直线y=![]() x上,⊙T上存在点B,使点Q是线段AB的“倍分点”,直接写出t的取值范围.
x上,⊙T上存在点B,使点Q是线段AB的“倍分点”,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
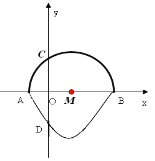
【题目】我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线。如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,点D的坐标为(0,-3)AB为半圆直径,半圆圆心M(1,0),半径为2,则经过点D的“蛋圆”的切线的解析式为__________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在四边形ABCD中,点E、F是对角线BD上的两点,且BE=FD.
(1)若四边形AECF是平行四边形,求证:四边形ABCD是平行四边形;
(2)若四边形AECF是菱形,那么四边形ABCD也是菱形吗?为什么?
(3)若四边形AECF是矩形,试判断四边形ABCD是否为矩形,不必写理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
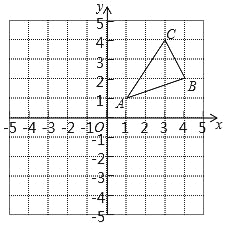
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC绕O点逆时针旋转90°得到△A1B1C1,请画出△A1B1C1.
(2)在x轴上求作一点P,使△PA1C1的周长最小,并直接写出P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com