
【题目】在平面直角坐标系xOy中,点A(x,0),B(x,y),若线段AB上存在一点Q满足![]() ,则称点Q是线段AB的“倍分点”.
,则称点Q是线段AB的“倍分点”.
(1)若点A(1,0),AB=3,点Q是线段AB的“倍分点”.
①求点Q的坐标;
②若点A关于直线y=x的对称点为A′,当点B在第一象限时,求![]() ;
;
(2)⊙T的圆心T(0,t),半径为2,点Q在直线y=![]() x上,⊙T上存在点B,使点Q是线段AB的“倍分点”,直接写出t的取值范围.
x上,⊙T上存在点B,使点Q是线段AB的“倍分点”,直接写出t的取值范围.
【答案】(1)①Q(1,1)或Q'(1,﹣1),②![]() ;(2)t的取值范围为﹣4≤t≤4
;(2)t的取值范围为﹣4≤t≤4
【解析】
(1) ①根据 “倍分点”的定义及A(1,0),AB=3,可得Q的坐标;②点A(1,0)关于直线y=x的对称点为A′(0,1),可得QA=QA′,可得答案;
(2)分①当A,B都在⊙T1上时,可得t的值,②当⊙T2上只有一个点Q是线段AB的“倍分点”时,过点T2作T2Q⊥图象L于点Q,交⊙T2于点N,过点Q作QD⊥x轴于点D,可得t的取值范围.
解:(1)如图1,
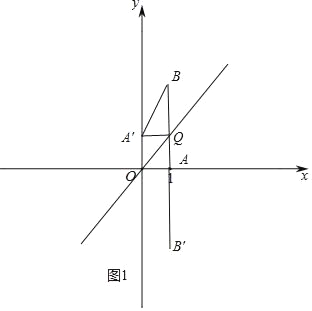
∵A(1,0),AB=3
∴B(1,3)或B'(1,﹣3)
∵![]()
∴Q(1,1)或Q'(1,﹣1)
(2)点A(1,0)关于直线y=x的对称点为A′(0,1),如图1,
∴QA=QA′
∴![]() ,
,
(3)①当A,B都在⊙T1上时,⊙T1与L没有交点,
∵⊙T1的半径为2,
∴此时点T1的坐标为(0,﹣4);
②当⊙T2上只有一个点Q是线段AB的“倍分点”时,过点T2作T2Q⊥图象L于点Q,交⊙T2于点N,过点Q作QD⊥x轴于点D,
∵图象L的解析式为y=![]() x(x>0),
x(x>0),
∴∠QOT=60°,∠OT2Q=30°.
∵点T2的坐标为(0,t),
∴OQ=![]() t,DQ=
t,DQ=![]() OQ=
OQ=![]() t,T2O=t.
t,T2O=t.
由“倍分点”的定义可知:OB=2DQ,即t﹣2=![]() t,
t,
解得:t=4,
综上所述:t的取值范围为﹣4≤t≤4.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,直角坐标平面内,小明站在点A(﹣10,0)处观察y轴,眼睛距地面1.5米,他的前方5米处有一堵墙DC,若墙高DC=2米,则小明在y轴上的盲区(即OE的长度)为_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两组卡片共5张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,5.它们除了数字外没有任何区别,
(1)随机从A组抽取一张,求抽到数字为2的概率;
(2)随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
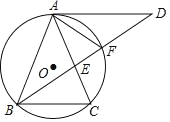
【题目】如图,△ABC内接于⊙O,AB=AC,∠BAC=36°,过点A作AD∥BC,与∠ABC的平分线交于点D,BD与AC交于点E,与⊙O交于点F.
(1)求∠DAF的度数;
(2)求证:AE2=EFED;
(3)求证:AD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=x+2与双曲线![]() 相交于点A(m,3).
相交于点A(m,3).
(1)求反比例函数的表达式;
(2)画出直线和双曲线的示意图;
(3)若P是坐标轴上一点,当OA=PA时.直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=![]() DQ,求点F的坐标.
DQ,求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
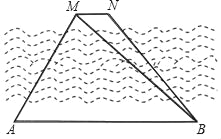
【题目】如图,在一条河的北岸有两个目标M、N,现在位于它的对岸设定两个观测点A、B.已知AB∥MN,在A点测得∠MAB=60°,在B点测得∠MBA=45°,AB=600米.
(1)求点M到AB的距离;(结果保留根号)
(2)在B点又测得∠NBA=53°,求MN的长.(结果精确到1米)
(参考数据:![]() ≈1.732,sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75)
≈1.732,sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:

(1)药物燃烧时,y关于x的函数关系式为________,自变量x的取值范为________;药物燃烧后,y关于x的函数关系式为________.
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过________分钟后,员工才能回到办公室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC在平面直角坐标系中,若x2﹣2![]() x+2=0的两根是x1、x2,且OC=x1+x2,OA=x1x2
x+2=0的两根是x1、x2,且OC=x1+x2,OA=x1x2
(1)求B点的坐标.
(2)把△ABC沿AC对折,点B落在点B′处,线段AB′与x轴交于点D,求直线BD的解析式.
(3)在平面上是否存在点P,使D、C、B、P四点形成的四边形为平形四边形?若存在,请直接写出P点坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com