
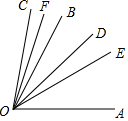
 已知∠BOC在∠AOB的外部,OE平分∠AOB,OF平分∠BOC,OD平分∠AOC,∠AOE=30°,∠BOD=20°,试求∠COF的度数,下面是李小雨同学的解题过程:
已知∠BOC在∠AOB的外部,OE平分∠AOB,OF平分∠BOC,OD平分∠AOC,∠AOE=30°,∠BOD=20°,试求∠COF的度数,下面是李小雨同学的解题过程:分析 分OD在∠AOB外部和∠AOB内部两种情况,①外部时,先根据角平分线定义得出∠COD=∠AOD=2∠AOE+∠BOD,继而由OF平分∠BOC可得∠COF=$\frac{∠COD+∠BOD}{2}$;②内部时,由OE平分∠AOB,∠AOE=30°,∠BOD=20°,可得∠AOD的值,再由OD平分∠AOC,可得出∠COD=∠AOD,由OF平分∠BOC,即可得出∠COF的值.
解答 解:不正确,
①如图1,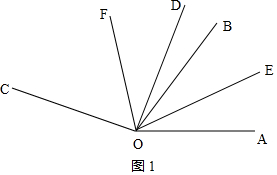
∵OE平分∠AOB,∠AOE=30°,∠BOD=20°,
∴∠AOD=30°+30°+20°=80°,
∵OD平分∠AOC,
∴∠COD=∠AOD=80°,
∴OF平分∠BOC,
∴∠COF=(80°+20°)÷2=50°.
②如图2,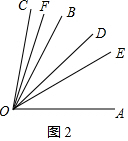
∵OE平分∠AOB,∠AOE=30°,∠BOD=20°,
∴∠AOD=30°+30°-20°=40°,
∵OD平分∠AOC,
∴∠COD=∠AOD=40°,
∴OF平分∠BOC,
∴∠COF=(40°-20°)÷2=10°.
点评 本题主要考查了角的计算及角平分线的定义,解题的关键是角平分线的灵活运用.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | 12 | B. | 16 | C. | $\frac{30}{17}\sqrt{34}$ | D. | $\frac{50}{17}\sqrt{34}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 任何有理数都有相反数 | |
| B. | 如果-15米表示向东前进了15米,那么10米表示向北前进了10米 | |
| C. | 离原点近的点所对应的有理数较小 | |
| D. | 有最大的负数,没有最小的正数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com