练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．分解因式
    （1）a3-ab2                      
    （2）a2+6ab+9b2．

    分析 （1）直接提取公因式a，进而利用平方差公式分解因式得出答案；
    （2）直接利用完全平方公式分解因式得出答案．

    解答 解：（1）a3-ab2=a（a2-b2）=a（a+b）（a-b）；

    （2）a2+6ab+9b2=（a+3b）2．

    点评 此题主要考查了提取公因式法以及公式法分解因式，正确运用公式是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．求下列式子中x的值：100x2-4=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．已知：如图，在△ABC中，∠C=90°，AE平分∠CAB，且BE2=DE•AE．求证：BE⊥AE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列说法中，错误的是（　　）
    A．长度为1的向量叫做单位向量
    B．如果k≠0，且$\overrightarrow{a}$≠$\overrightarrow{0}$，那么k$\overrightarrow{a}$的方向与$\overrightarrow{a}$的方向相同
    C．如果k=0或$\overrightarrow{a}$=$\overrightarrow{0}$，那么k$\overrightarrow{a}$=$\overrightarrow{0}$
    D．如果$\overrightarrow{a}$=$\frac{5}{2}$$\overrightarrow{c}$，$\overrightarrow{b}$=$\frac{1}{2}$$\overrightarrow{c}$，其中$\overrightarrow{c}$是非零向量，那么$\overrightarrow{a}$∥$\overrightarrow{b}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．计算 
    （1）（2a）2     
    （2）x6÷x4     
    （3）x0-（-1）2       
    （4）3x•2xy
    （5）（x+2）（x+3）
    （6）$\frac{m+3}{m+2}$-$\frac{1}{m+2}$   
    （7）（a+1）2-a（a-1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

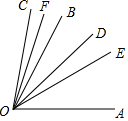    3．已知∠BOC在∠AOB的外部，OE平分∠AOB，OF平分∠BOC，OD平分∠AOC，∠AOE=30°，∠BOD=20°，试求∠COF的度数，下面是李小雨同学的解题过程：
    解：如图所示，
    因为OE平分∠AOB，
    所以∠BOE-∠AOE=30°，
    所以∠DOE=∠BOE-∠BOD=30°-20°=10°．
    ∠AOD=∠AOE+∠DOE=30°+10°=40°，
    因为OD平分∠AOC，
    所以∠COD=∠AOD=40°．
    所以∠BOC=∠COD-∠BOD=40°-20°=20°，
    又因为OF平分∠BOC，
    所以∠COF=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×20°=10°．
    请判断李小雨同学的解题过程是否正确，若不正确，请写出正确的解题过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

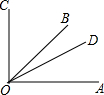    10．如图，已知∠COA=90°，∠COD比∠DOA大n°，且OB是∠COA的平分线．
    （1）若n=36，求∠BOD的度数；
    （2）直接用n的式子表示∠BOD为$\frac{1}{2}$n度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．如图，已知AB=6，C为AB的一个四等分点，D为BC的中点，则AD=（　　）
    A．$\frac{15}{4}$B．$\frac{15}{2}$C．4D．7

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

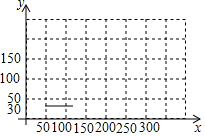    8．某电信公司提供的移动通讯服务的收费标准有两种方案，如表所示：
    A方案B方案
    每月基本服务费30元50元
    每月免费通话时间120分200分
    超出后每分钟收费0.4元0.4元
    设每月通话时间为x分，A，B两种方案每月话费分别为y1元，y2元．
    （1）分别写出当x＞120时，y1关于x的函数表达式和当x＞200时，y2关于x的函数表达式；
    （2）在如图所示的平面直角坐标系中，把y1和y2这两个函数图象的其余部分补画出来；（实线为A方案，虚线为B方案）
    （3）结合图象考虑，若以节省费用的角度考虑，则应如何选择最优方案？

    查看答案和解析>>

    同步练习册答案