
【题目】如图已知二次函数y=ax2图象的顶点为原点,直线y=![]() x+4的图象与该二次函数的图象交于A点(8,8),直线与x轴的交点为C,与y轴的交点为B.
x+4的图象与该二次函数的图象交于A点(8,8),直线与x轴的交点为C,与y轴的交点为B.
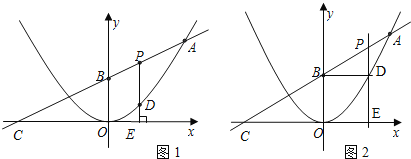
(1)求这个二次函数的解析式与B点坐标;
(2)P为线段AB上的一个动点(点P与A,B不重合),过P作x轴的垂线与这个二次函数的图象交于D点,与x轴交于点E.设线段PD的长为h,点P的横坐标为t,求h与t之间的函数关系式,并写出自变量t的取值范围(图1);
(3)在(2)的条件下,连接BD,当动点P在线段AB上移动时,点D也在抛物线上移动,线段BD也绕点B转动,当BD∥x轴时(图2),请求出P点的坐标.
【答案】(1)这个二次函数的解析式y=![]() x2.B点的坐标为(0,4).(2)h=﹣
x2.B点的坐标为(0,4).(2)h=﹣![]() t2+
t2+![]() t+4(0<t<8).(3)P点坐标为(4
t+4(0<t<8).(3)P点坐标为(4![]() ,4+2
,4+2![]() ).
).
【解析】
试题分析:(1)由二次函数的图象过点A(8,8),将其代入函数解析式中即可求得a值,将x=0代入直线方程,即可求得B点坐标;
(2)由P、D横坐标都为t,将其分别代入二次函数和直线解析式,用t表现出P、D点纵坐标,二者相减即可找到h与t的关系,因为P在线段BA上,由此可找出t的范围;
(3)BD平行x轴,可知,B、D两点纵坐标相等,从而求出t值,代入(2)中的P点坐标即可得出结论.
解:(1)∵二次函数y=ax2图象过点A(8,8),
∴有8=82a=64a,解得a=![]() ,
,
∴这个二次函数的解析式y=![]() x2.
x2.
∵点B为直线y=![]() x+4的图象与y轴的交点,
x+4的图象与y轴的交点,
∴当x=0时,y=![]() ×0+4=4,
×0+4=4,
∴B点的坐标为(0,4).
(2)∵P点在线段BA上,
∴P点坐标为(t,![]() t+4)(0<t<8),
t+4)(0<t<8),
∵D点在二次函数图象上,且P、D横坐标相等,
∴D点坐标为(t,![]() t2),
t2),
PD=h=![]() t+4﹣
t+4﹣![]() t2=﹣
t2=﹣![]() t2+
t2+![]() t+4(0<t<8).
t+4(0<t<8).
(3)∵当BD∥x轴时,B、D两点纵坐标相等,且B(0,4)
即4=![]() t2,
t2,
解得t=4![]() .
.
∴P点坐标为(4![]() ,4+2
,4+2![]() ).
).


 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】2016年11月17日,我国在酒泉卫星发射中心使用长征二号FY11运载火箭成功将神舟十一号载人飞船送入太空,此次神舟十一号顺利升空是中国航天的又一次重大胜利.神舟十一号和天宫二号对接时的轨道高度是393千米,比过去高了50千米.393千米可以用科学记数法表示为( )米.
A.3.93×105
B.3.93×106
C.3.93×104
D.0.393×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家.妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程S(km)与北京时间t(时)的函数图象如图所示.根据图象得到小亮结论,其中错误的是( )
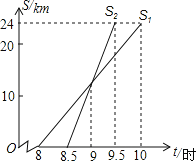
A.小亮骑自行车的平均速度是12km/h
B.妈妈比小亮提前0.5小时到达姥姥家
C.妈妈在距家12km处追上小亮
D.9:30妈妈追上小亮
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个口袋里有四个完全相同的小球,把它们分别标号为1,2,3,4,小明和小强采取的摸取方法分别是:
小明:随机摸取一个小球记下标号,然后放回,再随机摸取一个小球,记下标号;
小强:随机摸取一个小球记下标号,不放回,再随机摸取一个小球,记下标号.
(1)用画树状图(或列表法)分别表示小明和小强摸球的所有可能出现的结果;
(2)分别求出小明和小强两次摸球的标号之和等于5的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用白铁皮做罐头盒,每张铁片可制盒身16个或制盒底43个,一个盒身与两个盒底配成一套罐头盒,现有150张白铁皮,用多少张制盒身,多少张制盒底,可以正好制成整套罐头盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+bx+c过点A(1,4),B(﹣2,﹣5)
(1)求此抛物线的解析式;
(2)当y>0时,x的取值范围是 (直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按图填空, 并注明理由
已知: 如图, ∠1=∠2, ∠3=∠E. 求证: AD∥BE
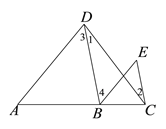
证明: ∵∠1 = ∠2 (已知)
∴ ∥ ( )
∴ ∠E = ∠ ( )
又∵ ∠E = ∠3 ( 已知 )
∴ ∠3 = ∠ ( 等量代换 )
∴ ∥ ( 内错角相等,两直线平行 )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com