Question

【题目】如图，在平面直角坐标系中，已知△AOB是等边三角形，点A的坐标是（0，4），点B在第一象限，点P是x轴上的一个动点，连接AP，并把△AOP绕着点A按逆时针方向旋转，使边AO与AB重合，得到△ABD．

（1）求B的坐标；

（2）当点P运动到点（t，0）时，试用含t的式子表示点D的坐标；

（3）是否存在点P，使△OPD的面积等于，若存在，请求出符合条件的点P的坐标（直接写出结果即可）

Answer 1

【答案】（1）点B的坐标是（2，2）．（2）点D的坐标为（，2+t）．（3）存在. 点P的坐标分别为P1（，0），P2（-，0），P3（-，0），P4（，0）．

【解析】

试题分析：（1）过点B作BE⊥y轴于点E，作BF⊥x轴于点F．依题意得BF=OE=2，利用勾股定理求出OF，然后可得点B的坐标．设直线AB的解析式是y=kx+b，把已知坐标代入可求解．

（2）由△ABD由△AOP旋转得到，△ABD≌△AOP，AP=AD，∠DAB=∠PAO，∠DAP=∠BAO=60°，△ADP是等边三角形，利用勾股定理求出DP．在Rt△BDG中，∠BGD=90°，∠DBG=60°．利用三角函数求出BG=BDcos60°，DG=BDsin60°．然后求出OH，DH，然后求出点D的坐标．

（3）分三种情况进行讨论：

①当P在x轴正半轴上时，即t＞0时；

②当P在x轴负半轴，但D在x轴上方时；即-＜t≤0时

③当P在x轴负半轴，D在x轴下方时，即t≤-时．

综合上面三种情况即可求出符合条件的t的值．

试题解析：（1）如图1，

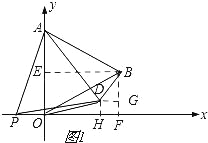
过点B作BE⊥y轴于点E，作BF⊥x轴于点F．

由已知得：BF=OE=2，

∴OF=，

∴点B的坐标是（2，2）．

设直线AB的解析式是y=kx+b（k≠0），

则有，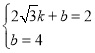

∴．

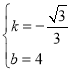∴直线AB的解析式是y=-x+4，

（2）∵△ABD由△AOP旋转得到，

∴△ABD≌△AOP．

∴AP=AD，∠DAB=∠PAO．

∴∠DAP=∠BAO=60°．

∴△ADP是等边三角形．

如图2，

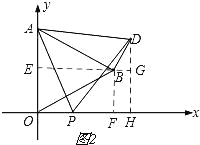
过点D作DH⊥x轴于点H，延长EB交DH于点G，则BG⊥DH．

在Rt△BDG中，∠BGD=90°，∠DBG=60°，

∴BG=BDcos60°=．DG=BDsin60°=t．

∴OH=EG=，DH=2+t．

∴点D的坐标为（，2+t）．

（3）存在．

假设存在点P，在它的运动过程中，使△OPD的面积等于．

设点P为（t，0），下面分三种情况讨论：

①当t＞0时，如答图2，BD=OP=t，DG=t，

∴DH=2+t．

∵△OPD的面积等于，

∴t（2+t）=，

∴t1=，t2=（舍去）．

∴点P1的坐标为（，0）．

②∵当D在x轴上时，如图3，

根据锐角三角函数求出BD=OP=，

∴当-＜t≤0时，如答图1，BD=OP=-t，DG=-t，

∴GH=BF=2-（-t）=2+t．

∵△OPD的面积等于

∴-t（2-t）=，

∴t1=-，t2=-

∴点P2的坐标为（-，0），点P3的坐标为（-，0）．

③当t≤-时，BD=OP=-t，DG=-t，

∴DH=-t-2．

∵△OPD的面积等于，

∴（-t）（-2-t）=，

∴t1=，t2=（舍去）．

∴点P4的坐标为（，0）．

综上所述，点P的坐标分别为P1（，0），P2（-，0），P3（-，0），P4（，0）．