Question

【题目】我们知道，三角形的内心是三条角平分线的交点，过三角形内心的一条直线与两边相交，两交点之间的线段把这个三角形分成两个图形．若有一个图形与原三角形相似，则把这条线段叫做这个三角形的“內似线”．

（1）等边三角形“內似线”的条数为　 　；

（2）如图，△ABC中，AB=AC，点D在AC上，且BD=BC=AD，求证：BD是△ABC的“內似线”；

（3）在Rt△ABC中，∠C=90°，AC=4，BC=3，E、F分别在边AC、BC上，且EF是△ABC的“內似线”，求EF的长．

Answer 1

【答案】(1)1；（2）证明见解析；（3）EF的长是.

【解析】试题分析：（1）过等边三角形的内心分别作三边的平行线，即可得出答案；

（2）由等腰三角形的性质得出∠ABC=∠C=∠BDC，证出△BCD∽△ABC即可；

（3）分两种情况：①当时，EF∥AB，由勾股定理求出AB==5，作DN⊥BC于N，则DN∥AC，DN是Rt△ABC的内切圆半径，求出DN=（AC+BC-AB）=1，由几啊平分线定理得出，求出CE=，证明△CEF∽△CAB，得出对应边成比例求出EF=；

②当时，同理得：EF=即可．

试题解析：（1）等边三角形“內似线”的条数为3条；理由如下：

过等边三角形的内心分别作三边的平行线，如图1所示：

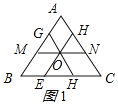
则△AMN∽△ABC，△CEF∽△CBA，△BGH∽△BAC，

∴MN、EF、GH是等边三角形ABC的內似线”；

（2）∵AB=AC，BD=BC，

∴∠ABC=∠C=∠BDC，

∴△BCD∽△ABC，

∴BD是△ABC的“內似线”；

（3）设D是△ABC的内心，连接CD，

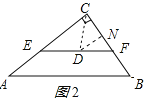
则CD平分∠ACB，

∵EF是△ABC的“內似线”，

∴△CEF与△ABC相似；

分两种情况：①当时，EF∥AB，

∵∠ACB=90°，AC=4，BC=3，

∴AB==5，

作DN⊥BC于N，如图2所示：

则DN∥AC，DN是Rt△ABC的内切圆半径，

∴DN=（AC+BC-AB）=1，

∵CD平分∠ACB，

∴，

∵DN∥AC，

∴，即，

∴CE=，

∵EF∥AB，

∴△CEF∽△CAB，

∴，即，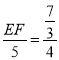

解得：EF=；

②当时，同理得：EF=；

综上所述，EF的长为．