Question

8．在直角坐标系中，A为x轴负半轴上的点，B为y轴负半轴上的点．
（1）如图①，以A点为顶点，AB为腰在第三象限作等腰Rt△ABC．若已知A（-2，0）B（0，-4），试求C点的坐标；
（2）如图②，若点A的坐标为（-2$\sqrt{3}$，0），点B的坐标为（0，a），点D的纵坐标为b，以B为顶点，BA为腰作等腰Rt△ABD，当B点沿y轴负半轴向下运动且其他条件都不变时，求式子2b-2a-4$\sqrt{3}$的值；
（3）如图③，E为x轴负半轴上的一点，且OB=OE，OF⊥EB于点F，以OB为边作等边△OBM，连接EM交OF于点N，求式子$\frac{EM-ON}{EN}$的值．

Answer 1

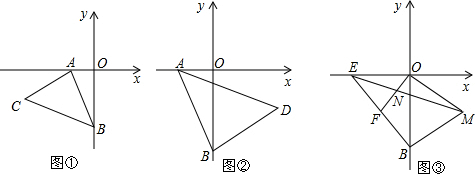
分析 （1）作CQ⊥OA于点Q，可以证明△AQC≌△BOA，由QC=AO，AQ=BO，再由条件就可以求出C的坐标．
（2）作DP⊥OB于点P，可以证明△AOB≌△BPD，则有AO=BP=OB-PO=-a-（-b）=b-a为定值，从而可以得出结论2b-2a-4$\sqrt{3}$的值不变为0；
（3）作BH⊥EB于B，由条件可以得出∠1=30°，∠2=∠3=∠EMO=15°，∠EOF=∠BMG=45°，EO=BM，可以证明△ENO≌△BGM，则GM=ON，就有EM-ON=EM-GM=EG，最后由平行线分线段成比例定理就可以得出EN=EM-ON的一半．

解答 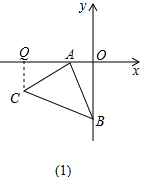解：（1）如图（1）作CQ⊥OA于点Q，
∴∠AQC=90°
∵△ABC等腰Rt△，
∴AC=AB，∠CAB=90°，
∴∠ACQ=∠BAO，
在△AQC与△BOA中，
$\left\{\begin{array}{l}{∠AQC=∠AOB}\\{∠QAC=∠ABO}\\{AC=AB}\end{array}\right.$，
∴△AQC≌△BOA，
∴CQ=AO，AQ=BO．
∵A（-2，0），B（0，-4），
∴OA=2，OB=4，
∴CQ=2，AQ=4，
∴OQ=6，
C（-6，-2）．

（2）如图（2）作DP⊥OB于点P，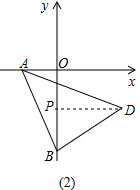
∴∠BPD=90°，
∵△ABD等腰Rt△，
∴AB=BD，∠ABD=∠ABO+∠OBD=90°，
∴∠ABO=∠BDP，
在△AOB与△BPD中，
$\left\{\begin{array}{l}{∠AOB=∠DPB}\\{∠ABO=∠PDB}\\{AB=BD}\end{array}\right.$，
∴△AOB≌△BPD，
∴AO=BP，
∵BP=OB-PO=-a-（-b）=b-a，
∴A（-2$\sqrt{3}$，0），
∴OA=2$\sqrt{3}$，
∴b-a=2$\sqrt{3}$，
∴当B点沿y轴负半轴向下运动时AO=BP=b-a=2$\sqrt{3}$，
∴整式2b-2a-4$\sqrt{3}$ 的值不变为0．

（3）证明：如图（3）在ME上截取MG=ON，连接BG，
∵△OBM是等边三角形，
∴BO=BM=MO，∠OBM=∠OMB=∠BOM=60°，
∴EO=MO，∠EBM=105°，∠1=30°，
∵OE=OB，
∴OE=OM=BM．
∴∠3=∠EMO=15°，
∴∠BEM=30°，∠BME=45°，
∵OF⊥EB，
∴∠EOF=45°
∴∠EOF=∠BME，
在△ENO与△BGM中，
$\left\{\begin{array}{l}{OE=BM}\\{∠EON=∠BMG}\\{ON=MG}\end{array}\right.$，
∴△ENO≌△BGM，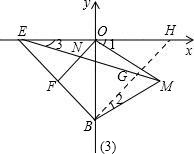
∴BG=EN．
∵ON=MG，
∴∠2=∠3，
∴∠2=15°，
∴∠EBG=90°
∴BG=$\frac{1}{2}$EG，
∴EN=$\frac{1}{2}$EG，
∵EG=EM-GM，
∴EN=$\frac{1}{2}$（EM-GM），
∴EN=$\frac{1}{2}$（EM-ON），
∴$\frac{EM-ON}{EN}$=$\frac{1}{2}$．

点评 本题考查了等腰直角三角形的性质，等边三角形的性质，等腰三角形的性质，三角形的外角与内角的关系，全等三角形的判定与性质，平行线等分线段定理，正确的作出辅助线是解题的关键．