
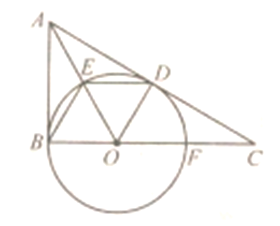
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上一点.以
边上一点.以![]() 为圆心
为圆心![]() 长为半径的⊙O与
长为半径的⊙O与![]() 边相切于
边相切于![]() 点,与边
点,与边![]() 相交于点
相交于点![]() ,连接
,连接![]() 交⊙O于点
交⊙O于点![]() ,连接
,连接![]() .
.
(1)求证:![]() .
.
(2)若⊙O的半径为![]() .
.
①当![]() 的长为 时,四边形
的长为 时,四边形![]() 为菱形;
为菱形;
②若![]() .则
.则![]() 的长为 .
的长为 .
【答案】(1)证明见解析;(2)①![]() ;②
;②![]()
【解析】
(1)利用全等三角形的判定证明![]() 即可证明结论;
即可证明结论;
(2)①运用菱形的性质可得![]() 均为等边三角形,即可得出∠BOD的度数,即可求得
均为等边三角形,即可得出∠BOD的度数,即可求得![]() 的长;
的长;
②利用勾股定理求出CD的长度,再利用勾股定理列出方程,求解即可得出答案.
(1)∵⊙O与![]() 边相切于
边相切于![]() 点,
点,
∴∠ADO=90°,
∴∠ADO=∠ABO=90°,
又∵OB=OD,OA=OA,
∴![]() ,
,
∴∠AOB=∠AOD,
∴![]() ,
,
∴BE=ED.
(2)①∵四边形![]() 为菱形,
为菱形,
∴BE=BO=ED=OD,
∵OB=OE,
∴OB=OE=BE,OE=ED=OD,
∴![]() 均为等边三角形,
均为等边三角形,
∴∠BOE=∠EOD=60°,
∴∠BOD=120°,
∴![]() 的长为
的长为![]() ,
,
∴![]() 的长为
的长为![]() 时,四边形
时,四边形![]() 为菱形.
为菱形.
故答案为:![]() .
.
②设AD=x,
∵![]() ,
,
∴AB=AD=x,
在![]() 中,OC=3+2=5,OD=3,
中,OC=3+2=5,OD=3,
∴CD=![]() ,
,
∴AC=x+4,
在Rt△ABC中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
故答案为:6.


科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
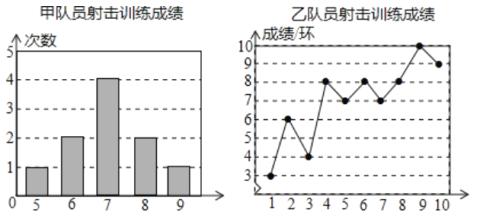
根据以上信息,整理分析数据如下:
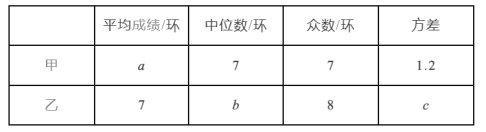
(1)写出表格中![]() 的值;
的值;
(2)综合运用上表中的四个统计量,简要分析这两名队员的射击训练成绩,若选派其中一名参赛,你认为应该选哪名队员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知OA是⊙O的半径,OA=1,点P是OA上一动点,过P作弦BC⊥OA,连接AB、AC.

(1)如图1,若P为OA中点,则AC=______,∠ACB=_______°;
(2)如图2,若移动点P,使AB、CO的延长线交于点D.记△AOC的面积为S1,△BOD的面积为S2.△AOD的面积为S3,且满足![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
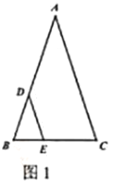
【题目】黄金三角形就是一个等腰三角形,且其底与腰的长度比为黄金比值![]() .如图1,在黄金
.如图1,在黄金![]() 中,
中,![]() ,点
,点![]() 是
是![]() 上的一动点,过点
上的一动点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
![]() 当点
当点![]() 是线段
是线段![]() 的中点时,
的中点时,![]() ;当点
;当点![]() 是线段
是线段![]() 的三等分点时,
的三等分点时,![]() ;
;
![]() 把
把![]() 绕点
绕点![]() 逆时针旋转到如图2所示位置,连接
逆时针旋转到如图2所示位置,连接![]() ,判断
,判断![]() 的值是否变化,并给出证明;
的值是否变化,并给出证明;
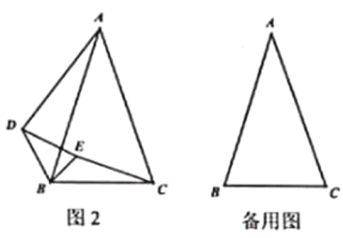
![]() 把
把![]() 绕点
绕点![]() 在平面内自由旋转,若
在平面内自由旋转,若![]() 请直接写出线段
请直接写出线段![]() 的长的取值范围.
的长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一条直线把矩形分割成两个矩形,其中一个为黄金矩形 (宽与长的比为![]() 的矩形),则称这条直线为该矩形的黄金线.例如图所示的矩形
的矩形),则称这条直线为该矩形的黄金线.例如图所示的矩形![]() 中,直线
中,直线![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,且
,且![]() ,显然直线
,显然直线![]() 是矩形
是矩形![]() 的黄金线.
的黄金线.
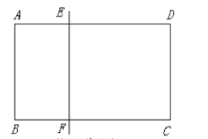
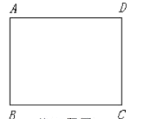
(1)如图,在矩形![]() 中,
中,![]() ,
,![]() .请在图中画出矩形
.请在图中画出矩形![]() 的其中一条黄金线
的其中一条黄金线![]() ,其中
,其中![]() 在
在![]() 边上,
边上,![]() 在
在![]() 边上,并标注出线段
边上,并标注出线段![]() 的长度;
的长度;
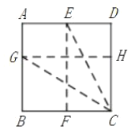
(2)将正方形纸片按图所示的方式折叠.
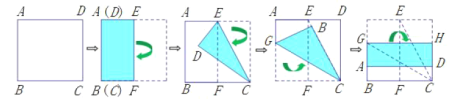
如图所示,按上述方法折叠所得到的折痕![]() 是否为正方形
是否为正方形![]() 的黄金线?请说明理由.
的黄金线?请说明理由.
(3)在矩形![]() 中,
中,![]() ,
,![]() ,己知矩形
,己知矩形![]() 的黄金线
的黄金线![]() 恰好将矩形
恰好将矩形![]() 分割成两个黄金矩形,则
分割成两个黄金矩形,则![]() ______(只要求直接写出其中三个答案).
______(只要求直接写出其中三个答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣![]() x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.
x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.

(1)求该抛物线的解析式;
(2)P是抛物线上一动点(不与点A、B重合),
①如图2,若点P在直线AB上方,连接OP交AB于点D,求![]() 的最大值;
的最大值;
②如图3,若点P在x轴的上方,连接PC,以PC为边作正方形CPEF,随着点P的运动,正方形的大小、位置也随之改变.当顶点E或F恰好落在y轴上,直接写出对应的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,P是边BC上的一动点(不与点B,C重合),点B关于直线AP的对称点为E,连接AE,连接DE并延长交射线AP于点F,连接BF
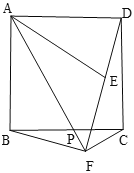
(1)若![]() ,直接写出
,直接写出![]() 的大小(用含
的大小(用含![]() 的式子表示).
的式子表示).
(2)求证:![]() .
.
(3)连接CF,用等式表示线段AF,BF,CF之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红旗连锁超市准备购进甲、乙两种绿色袋装食品.甲、乙两种绿色袋装食品的进价和售价如表.已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
甲 | 乙 | |
进价(元/袋) |
|
|
售价(元/袋) | 20 | 13 |
(1)求![]() 的值;
的值;
(2)要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价-进价)不少于4800元,且不超过4900元,问该超市有几种进货方案?
(3)在(2)的条件下,该超市如果对甲种袋裝食品每袋优惠![]() 元出售,乙种袋装食品价格不变.那么该超市要获得最大利润应如何进货?
元出售,乙种袋装食品价格不变.那么该超市要获得最大利润应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC在平面直角坐标系内,三个顶点的坐标分别为A(0,3),B(4,5),C(3,2).(正方形网格中,每个小正方形的边长都是1个单位长度)
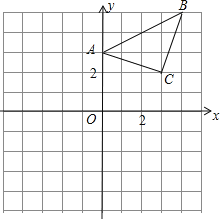
(1)画出△ABC向下平移5个单位长度得到的![]() ,并直接写出点
,并直接写出点![]() 的坐标;
的坐标;
(2)以点B为位似中心,在网格中画出![]() ,使
,使![]() 与
与![]() 位似,且相似比为2∶1,并直接写出
位似,且相似比为2∶1,并直接写出![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com