
分析 △COD的周长=OC+OD+CD,根据平行四边形的对角线互相平分的性质求得OC与OD的长,根据平行四边形的对边相等可得CD=AB=25,进而求得答案.
解答  解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,
∴OC=OA=$\frac{1}{2}$AC=14,OD=OB=$\frac{1}{2}$BD=23,CD=AB=25,
∴△COD的周长=OC+OD+CD=14+23+25=62.
故答案为62.
点评 本题重点考查了平行四边形的性质,并利用性质解题.平行四边形基本性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.熟记性质是解题的关键.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:解答题
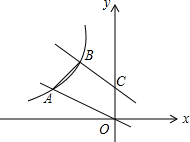 直线y=-x+1交y轴于C点,直线y=-$\frac{1}{2}$x,两条直线分别交双曲线y=$\frac{k}{x}$(x<0)于B、A两点,若$\frac{OA}{BC}$=$\frac{\sqrt{10}}{2}$.
直线y=-x+1交y轴于C点,直线y=-$\frac{1}{2}$x,两条直线分别交双曲线y=$\frac{k}{x}$(x<0)于B、A两点,若$\frac{OA}{BC}$=$\frac{\sqrt{10}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某水产公司建了一个水池,用来临时存放活鱼,中间用两块隔板将水池分隔成甲、乙、丙三个水池,每块隔板在距离底面50厘米处都开一个方孔,且甲、丙的底面积相同,乙的底面积是甲的4倍,一次在清理水池后,甲池有10厘米深的水,现用两支水枪A,B,以相同的速度,同时分别向乙、丙水池注水,1分钟后,丙池水深40厘米.则甲、乙两池水深相差5厘米时所用的时间是( )
某水产公司建了一个水池,用来临时存放活鱼,中间用两块隔板将水池分隔成甲、乙、丙三个水池,每块隔板在距离底面50厘米处都开一个方孔,且甲、丙的底面积相同,乙的底面积是甲的4倍,一次在清理水池后,甲池有10厘米深的水,现用两支水枪A,B,以相同的速度,同时分别向乙、丙水池注水,1分钟后,丙池水深40厘米.则甲、乙两池水深相差5厘米时所用的时间是( )| A. | 0.5分钟 | B. | 1.5分钟 | ||
| C. | 0.5分钟或$\frac{11}{8}$分钟 | D. | 0.5分钟或$\frac{11}{8}$分钟或$\frac{59}{16}$分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 11 | B. | 12 | C. | 14 | D. | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com