
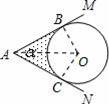
如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是( )


A.
 B.
B.
 C.
C.
 D.
D.

C【考点】动点问题的函数图象;多边形内角与外角;切线的性质;切线长定理;扇形面积的计算;锐角三角函数的定义.
【专题】计算题;压轴题.
【分析】连接OB、OC、OA,求出∠BOC的度数,求出AB、AC的长,求出四边形OBAC和扇形OBC的面积,即可求出答案.
【解答】解:连接OB、OC、OA,
∵圆O切AM于B,切AN于C,
∴∠OBA=∠OCA=90°,OB=OC=r,AB=AC
∴∠BOC=360°﹣90°﹣90°﹣α=(180﹣α)°,
∵AO平分∠MAN,
∴∠BAO=∠CAO=
 α,
α,
AB=AC=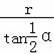
 ,
,
∴阴影部分的面积是:S四边形BACO﹣S扇形OBC=2×
 ×
×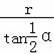
 ×r﹣
×r﹣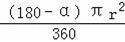
 =(
=(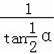
 ﹣
﹣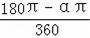
 )r2,
)r2,
∵r>0,
∴S与r之间是二次函数关系.
故选C.

【点评】本题主要考查对切线的性质,切线长定理,三角形和扇形的面积,锐角三角函数的定义,四边形的内角和定理等知识点的理解和掌握,能综合运用性质进行计算是解此题的关键.


科目:初中数学 来源: 题型:
如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD的中点E,AE的延长线与BC的延长线交于点P.
(1)求证:AP是⊙O的切线;
(2)OC=CP,AB=6,求CD的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC中,∠ABC=90°.
(1)请在BC上找一点P,作⊙P与AC,AB都相切,切点为Q;(尺规作图,保留作图痕迹)
(2)若AB=3,BC=4,求第(1)题中所作圆的半径;
(3)连结BQ,第(2)中的条件均不变,求sin∠CBQ.


查看答案和解析>>
科目:初中数学 来源: 题型:
反比例函数y=
 的图象如图所示,以下结论正确的是( )
的图象如图所示,以下结论正确的是( )
①常数m<1;
②y随x的增大而减小;
③若A为x轴上一点,B为反比例函数上一点,则S△ABC=
 ;
;
④若P(x,y)在图象上,则P′(﹣x,﹣y)也在图象上.


A.①②③ B.①③④ C.①②③④ D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com