Question

为了更好治理流溪河水质，保护环境，市治污公司决定购买10台污水处理设备．现有A，B两种型号的设备，其中每台的价格，月处理污水量如表：

	A型	B型
价格（万元/台）	a	b
处理污水量（吨/月）	240	200

 

经调查：购买一台A型设备比购买一台B型设备多2万元，购买2台A型设备比购买3台B型设备少6万元．

（1）求a，b的值．

（2）经预算：市治污公司购买污水处理设备的资金不超过105万元，你认为该公司有哪几种购买方案．

（3）在（2）问的条件下，若每月要求处理流溪河两岸的污水量不低于2040吨，为了节约资金，请你为治污公司设计一种最省钱的购买方案．

 

Answer 1

（1）a=12，b=10；（2）有三种购买方案：①A型设备0台，B型设备10台；②A型设备1台，B型设备9台；③A型设备2台，B型设备8台．（3）为了节约资金，应选购A型设备1台，B型设备9台．

【解析】

试题分析：（1）根据“购买一台A型设备比购买一台B型设备多2万元，购买2台A型设备比购买3台B型设备少6万元”即可列出方程组，继而进行求解；

（2）可设购买污水处理设备A型设备x台，B型设备（10-x）台，则有12x+10（10-x）≤105，解之确定x的值，即可确定方案；

（3）因为每月要求处理流溪河两岸的污水量不低于2040吨，所以有240x+200（10-x）≥2040，解之即可由x的值确定方案，然后进行比较，作出选择．

试题解析：（1）根据题意得：

，

∴；

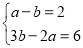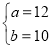（2）设购买污水处理设备A型设备x台，B型设备（10-x）台，

则：12x+10（10-x）≤105，

∴x≤2.5，

∵x取非负整数，

∴x=0，1，2，

∴有三种购买方案：

①A型设备0台，B型设备10台；

②A型设备1台，B型设备9台；

③A型设备2台，B型设备8台．

（3）由题意：240x+200（10-x）≥2040，

∴x≥1，

又∵x≤2.5，x取非负整数，

∴x为1，2．

当x=1时，购买资金为：12×1+10×9=102（万元），

当x=2时，购买资金为：12×2+10×8=104（万元），

∴为了节约资金，应选购A型设备1台，B型设备9台．

考点：1.一元一次不等式的应用；2.二元一次方程组的应用．