
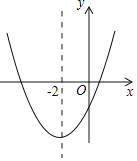
����Ŀ�����κ���y��ax2+bx+c��a��0���Ĵ���ͼ����ͼ��ʾ����������Ϊ����2����9a�������н��ۣ���abc��0����4a+2b+c��0����5a��b+c��0����������a��x+5����x��1������1��������x1��x2����x1��x2����5��x1��x2��1����������|ax2+bx+c|��1���ĸ����������ĸ����ĺ�Ϊ��8��������ȷ�Ľ����У�������
A.�٢ڢۢ�B.�٢ڢۢ�C.�ڢۢܢ�D.�٢ڢܢ�
���𰸡�D
��������
���ݿ��ڷ��Գ��ᡢ��y��Ľ�����жϢ٣����ݶ�������Ϊ����2����9a�������b��c��a�Ĺ�ϵ�����жϢںۣ͢��������������x��Ľ��㣬���жϢܣ����ݸ���ϵ���Ĺ�ϵ���жϢݣ�
�⣺�������ߵĿ������ϣ���a��0���Գ�����y�����࣬��b��0����y��ĸ����ᣬ��c��0��
��abc��0�����Ԣٽ�����ȷ��
�������ߵĶ�������(-2��-9a)��
��![]() ��
��![]() ��
��
��b=4a��c=-5a��
�������ߵĽ���ʽΪy=ax2+4ax-5a��
��4a+2b+c=4a+8a-5a=7a��0�����Ԣڽ�����ȷ��
5a-b+c=5a-4a-5a=-4a��0���ʢ۽�����ȷ��
���ڷ���ax2+4ax-5a=0��
��a��0��
��x2+4x-5=0��
���x1=-5��x2=1��
��������y=ax2+4ax-5a��x����(-5��0)��(1��0)��
��������a(x+5)(x-1)=-1��������x1��x2����x1��x2����-5��x1��x2��1���ʽ��ۢ���ȷ��
������|ax2+bx+c|=1���ĸ������跽��ax2+bx+c=1�������ֱ�Ϊx1��x2����![]() ���ɵ�x1+x2=-4���跽��ax2+bx+c=-1�������ֱ�Ϊx3��x4����
���ɵ�x1+x2=-4���跽��ax2+bx+c=-1�������ֱ�Ϊx3��x4����![]() ���ɵ�x3+x4=-4���������ĸ����ĺ�Ϊ-8���ʽ��ۢ���ȷ��
���ɵ�x3+x4=-4���������ĸ����ĺ�Ϊ-8���ʽ��ۢ���ȷ��
��ѡ��D��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
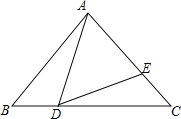
����Ŀ����ͼ����![]() �У���BAC=90����AB=AC=2����
�У���BAC=90����AB=AC=2����![]() �ֱ���
�ֱ���![]() �ϣ���
�ϣ���![]() �����
�����![]() �غϣ�����
�غϣ�����![]() 45������
45������![]() �ǵ��������Σ���
�ǵ��������Σ���![]() ______��
______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
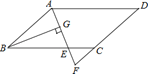
����Ŀ����ͼ����ABCD�У�AB=6��AD=9����BAD��ƽ���߽�BC�ڵ�E����DC���ӳ����ڵ�F��BG��AE������ΪG����BG=![]() ������CEF������ǣ�������
������CEF������ǣ�������
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
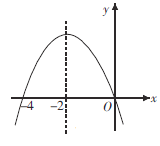
����Ŀ����ͼ�Ƕ��κ���![]() ͼ���һ���֣��Գ�����ֱ��x=��2.�������н��ۣ���ab<0����
ͼ���һ���֣��Գ�����ֱ��x=��2.�������н��ۣ���ab<0����![]() ����
����![]() ����
����![]() ���ݷ���
���ݷ���![]() ��������Ϊ
��������Ϊ![]() ��
��![]() ������ȷ�Ľ����У� ��
������ȷ�Ľ����У� ��
A.�٢ۢ�B.�ڢܢ�C.�٢ڢ�D.�ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ƽ���ı���ABCD���Խ���AC��BD�ཻ�ڵ�E����GΪAD���е㣬����CG��CG���ӳ��߽�BA���ӳ����ڵ�F������FD��
��1����֤��AB=AF��
��2����AG=AB����BCD=120�㣬�ж��ı���ACDF����״����֤����Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2+��2m+1��x+m2��2��0��
��1�����÷���������ʵ��������m����С����ֵ��
��2�������̵�����ʵ����Ϊx1��x2���ң�x1��x2��2+m2��21����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һũ��Ҫ��һ���������ᣬ�����һ�����ó�Ϊ15m��ס��ǽ������������27m���Ľ�������Χ�ɣ�Ϊ����������ڴ�ֱ��ס��ǽ��һ����һ��1m�����ţ���Χ��������ij������ֱ�Ϊ������ʱ���������Ϊ96m2��
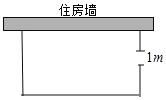
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ˮ����λ�ڵ��ֺӺ���ۺ�����ڣ��ǻ���ˮϵ�����ֺ��ε���������Ҫ�ı�־�Ծ��ۣ��ڿ���ʵ����У�ijУ���꼶��ѧ��ȤС�����������ˮ���ŵĸߣ����ǵIJ����������£���ͼ������D����õ�A������Ϊ20��������ˮ���ŵķ���ǰ��13����C������õ�A������Ϊ31������D��C��B��һֱ���ϣ������ˮ����AB�ĸߣ�����ȷ��0.1�ף�
���ο����ݣ�sin20���0.34��cos20���0.94��tan20���0.36��sin31���0.52��cos31���0.86��tan31���0.60��
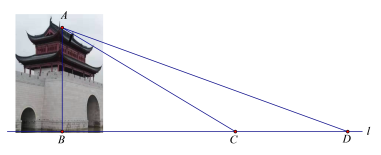
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ��ֱ��
��ֱ��![]() �������߽��ڵ�
�������߽��ڵ�![]() ��
��![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��
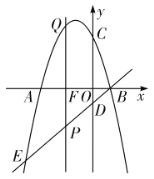
��1���������ߵĽ���ʽ��
��2����![]() ���߶�
���߶�![]() �ϵ�һ���㣨����
�ϵ�һ���㣨����![]() ��
��![]() �غϣ�������
�غϣ�������![]() ��
��![]() ��Ĵ��ߣ���
��Ĵ��ߣ���![]() ���ڵ�
���ڵ�![]() �����������ڵ�
�����������ڵ�![]() ����
����![]() ���߶�
���߶�![]() �Ƿ�������ֵ�������ڣ���������ֵ���������ڣ���˵�����ɣ�
�Ƿ�������ֵ�������ڣ���������ֵ���������ڣ���˵�����ɣ�
��3����![]() ���ϴ���һ��
���ϴ���һ��![]() ��ʹ��
��ʹ��![]() ʱ�������
ʱ�������![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com