
如图所示,在梯形ABCD中,AD∥BC,AB=CD,E、F、G、H分别为边AB、BC、CD、DA的中点,求证:四边形EFGH为菱形.
连接AC、BD,根据等腰梯形的对角线相等可得AC=BD,再根据三角形的中位线平行于第三边并且等于第三边的一半求出EF=GH=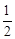 AC,HE=FG=
AC,HE=FG=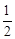 BD,从而得到EF=FG=GH=HE,再根据四条边都相等的四边形是菱形判定即可。
BD,从而得到EF=FG=GH=HE,再根据四条边都相等的四边形是菱形判定即可。
解析分析:连接AC、BD,根据等腰梯形的对角线相等可得AC=BD,再根据三角形的中位线平行于第三边并且等于第三边的一半求出EF=GH=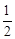 AC,HE=FG=
AC,HE=FG=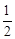 BD,从而得到EF=FG=GH=HE,再根据四条边都相等的四边形是菱形判定即可。
BD,从而得到EF=FG=GH=HE,再根据四条边都相等的四边形是菱形判定即可。
证明:如图,连接AC、BD,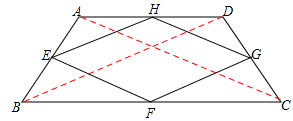
∵AD∥BC,AB=CD,∴AC=BD。
∵E、F、G、H分别为边AB、BC、CD、DA的中点,
∴在△ABC中,EF=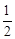 AC;在△ADC中,GH=
AC;在△ADC中,GH=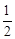 AC,
AC,
∴EF=GH=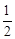 AC。
AC。
同理可得,HE=FG=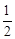 BD。∴EF=FG=GH=HE。
BD。∴EF=FG=GH=HE。
∴四边形EFGH为菱形,


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:北师大版(新课标) 九年级(上) 题型:
| |||||||||||||||
查看答案和解析>>
科目:初中数学 来源:2015届初中数学苏教版八年级上册第一章练习卷(解析版) 题型:选择题
如图,在△ABC中,点D是BC的中点,作射线AD,在线段AD及其延长线上分别取点E,F,连结CE,BF.添加一个条件,使得△BDF≌△CDE,你添加的条件是 (不添加辅助线).

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,一个平行四边形的活动框架,对角线是两根橡皮筋.若改变框架的形状,则∠α也随之变化,两条对角线长度也在发生改变.当∠α为 度时,两条对角线长度相等.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图所示,将长方形ABCD沿直线BD折叠,使C点落在C′处,BC′交AD于E.
(1)求证:BE=DE;
(2)若AD=8,AB=4,求△BED的面积.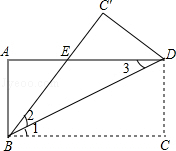
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6 ,AF=4
,AF=4 ,求AE的长.
,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com