
【题目】如图,已知点A是反比例函数 ![]() 的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为 .
的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为 . 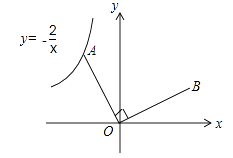
【答案】![]()
【解析】∵点A是反比例函数 ![]() 的图象上的一个动点,设A(m,n),过A作AC⊥x轴于C,过B作BD⊥x轴于D,
的图象上的一个动点,设A(m,n),过A作AC⊥x轴于C,过B作BD⊥x轴于D,
∴AC=n,OC=﹣m,
∴∠ACO=∠ADO=90°,
∵∠AOB=90°,
∴∠CAO+∠AOC=∠AOC+∠BOD=90°,
∴∠CAO=∠BOD,
在△ACO与△ODB中,
∵∠ACO=∠ODB,∠CAO=∠BOD,AO=BO,
∴△ACO≌△ODB,
∴AC=OD=n,CO=BD=﹣m,
∴B(n,﹣m),
∵mn=﹣2,
∴n(﹣m)=2,
∴点B所在图象的函数表达式为 ![]() ,
,
故答案为: ![]() .
.
过A作AC⊥x轴于C,过B作BD⊥x轴于D,根据旋转的性质得出AO=BO,再证明∠ACO=∠ODB,∠CAO=∠BOD,可得出OC=BD,AC=OD,然后求出mn的值即可得出点B所在图象的函数解析式。


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
(1)求证:△ABF∽△BEC;
(2)若AD=5,AB=8,sinD= ![]() ,求AF的长.
,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课外兴趣小组活动时,老师提出了如下问题:
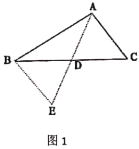
(1)如图1,![]() 中,若
中,若![]() ,
,![]() ,求
,求![]() 边上的中线
边上的中线![]() 的取值范围.小明在组内经过合作交流,得到了如下的解决方法:将
的取值范围.小明在组内经过合作交流,得到了如下的解决方法:将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,把
,把![]() 、
、![]() 、
、![]() 集中在
集中在![]() 中,利用三角形的三边关系可得
中,利用三角形的三边关系可得![]() ,则
,则![]() ;
;
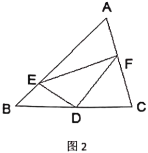
(2)问题解决:受到(1)的启发,请你证明下面命题:如图2,在![]() 中,
中,![]() 是
是![]() 边上的中点,
边上的中点,![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
①求证:![]() ;
;
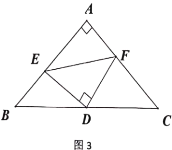
②如图3,若![]() ,探索线段
,探索线段![]() 、
、![]() 、
、![]() 之间的等量关系,并加以证明.
之间的等量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
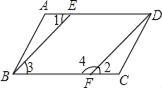
【题目】如图,已知AD∥BC,∠3+∠4=180°,要证∠1=∠2,请完善证明过程,并在括号内填上相应依据:
∵AD∥BC(已知)
∴∠l=∠3( ),
∵∠3+∠4=180°(已知),
∴BE∥DF( ),
∴ = ( ).
∴∠1=∠2( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AE⊥BC,CF⊥AD,垂足分别为E,F,AE,CF分别与BD交于点G和H,且AB= ![]() .
.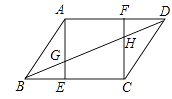
(1)若tan∠ABE =2,求CF的长;
(2)求证:BG=DH.
查看答案和解析>>
科目:初中数学 来源: 题型:
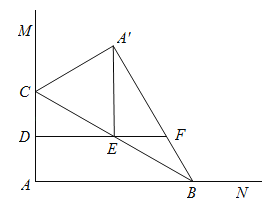
【题目】如图,![]() 点
点![]() 在边
在边![]() 上,
上,![]() 点
点![]() 为边
为边![]() 上一动点,连接
上一动点,连接![]() 与
与![]() 关于
关于![]() 所在直线对称,点
所在直线对称,点![]() 分别为
分别为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 所在直线于点
所在直线于点![]() ,连接
,连接![]() .当
.当![]() 为直角三角形时,
为直角三角形时,![]() 的长为_________ .
的长为_________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
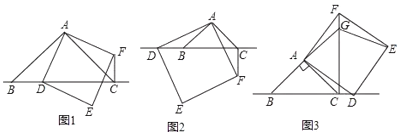
【题目】类比思想就是根据已经学习过的知识,类比探究新知识的思想方法.我们在探究矩形、菱形、正方形等问题中的数量关系时,经常用到类比思想.某数学兴趣小组在数学课外活动中,研究三角形和正方形的性质时,做了如下探究:在![]() 中,
中,![]() 点
点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与
不与![]() 重合),以
重合),以![]() 为边在
为边在![]() 右侧作正方形
右侧作正方形![]() 连接
连接![]() .
.
(1)(观察猜想)如图①,当点![]() 在线段
在线段![]() 上时;
上时;
①![]() 与
与![]() 的位置关系为: ;
的位置关系为: ;
②![]() 之间的数量关系为: ;(将结论直接写在横线上)
之间的数量关系为: ;(将结论直接写在横线上)
(2)(数学思考)如图②,当点![]() 在线段
在线段![]() 的延长线上时,结论①②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
的延长线上时,结论①②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
(3)(拓展延伸)如图③,当点![]() 在线段
在线段![]() 的延长线上时,延长
的延长线上时,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .若已知
.若已知![]() 请直接写出
请直接写出![]() 的长.(提示: .过
的长.(提示: .过![]() 作
作![]() 于
于![]() 过
过![]() 作
作![]() 于
于![]() 于
于![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,地面上小山的两侧有A,B两地,为了测量A,B两地的距离,让一热气球从小山西侧A地出发沿与AB成30°角的方向,以每分钟40m的速度直线飞行,10分钟后到达C处,此时热气球上的人测得CB与AB成70°角,请你用测得的数据求A,B两地的距离AB长.(结果用含非特殊角的三角函数和根式表示即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com