
【题目】如图,已知抛物线![]() (a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.
(a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.

(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点B的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且△MAC为等腰三角形,请直接写出所有符合条件的点M的坐标.
【答案】(1)![]() ;(2)P(1,0);(3).
;(2)P(1,0);(3).
【解析】
试题(1)直接将A、B、C三点坐标代入抛物线的解析式中求出待定系数即可;
(2)由图知:A.B点关于抛物线的对称轴对称,那么根据抛物线的对称性以及两点之间线段最短可知,直线l与x轴的交点,即为符合条件的P点;
(3)由于△MAC的腰和底没有明确,因此要分三种情况来讨论:①MA=AC、②MA=MC、③AC=MC;可先设出M点的坐标,然后用M点纵坐标表示△MAC的三边长,再按上面的三种情况列式求解.
试题解析:(1)将A(﹣1,0)、B(3,0)、C(0,﹣3)代入抛物线![]() 中,得:
中,得: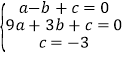 ,解得:
,解得: ,故抛物线的解析式:
,故抛物线的解析式:![]() .
.
(2)当P点在x轴上,P,A,B三点在一条直线上时,点P到点A、点B的距离之和最短,此时x=![]() =1,故P(1,0);
=1,故P(1,0);
(3)如图所示:抛物线的对称轴为:x=![]() =1,设M(1,m),已知A(﹣1,0)、C(0,﹣3),则:
=1,设M(1,m),已知A(﹣1,0)、C(0,﹣3),则:
![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,![]() =10;
=10;
①若MA=MC,则![]() ,得:
,得:![]() =
=![]() ,解得:m=﹣1;
,解得:m=﹣1;
②若MA=AC,则![]() ,得:
,得:![]() =10,得:m=
=10,得:m=![]() ;
;
③若MC=AC,则![]() ,得:
,得:![]() =10,得:
=10,得:![]() ,
,![]() ;
;
当m=﹣6时,M、A、C三点共线,构不成三角形,不合题意,故舍去;
综上可知,符合条件的M点,且坐标为 M(1,![]() )(1,
)(1,![]() )(1,﹣1)(1,0).
)(1,﹣1)(1,0).



科目:初中数学 来源: 题型:
【题目】为了解家长对“学生在校带手机”现象的看法,某校“九年级兴趣小组”随机调查了该校学生家长若干名,并对调查结果进行整理,绘制如下不完整的统计图:
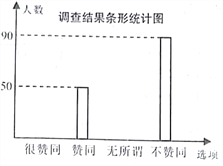
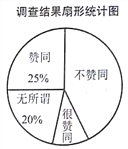
请根据以上信息,解答下列问题
(1)这次接受调查的家长总人数为________人;
(2)在扇形统计图中,求“很赞同”所对应的扇形圆心角的度数;
(3)若在这次接受调查的家长中,随机抽出一名家长,恰好抽到“无所谓”的家长概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
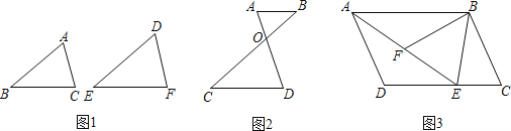
【题目】 先阅读下面的材料,再解答下面的问题:如果两个三角形的形状相同,则称这两个三角形相似.如图1,△ABC与△DEF形状相同,则称△ABC与△DEF相似,记作△ABC∽△DEF.那么,如何说明两个三角形相似呢?我们可以用“两角分别相等的三角形相似”加以说明.用数学语言表示为:
如图1:在△ABC与△DEF中,∵∠A=∠D,∠B=∠E,∴△ABC∽△DEF.
请你利用上述定理解决下面的问题:
(1)下列说法:①有一个角为50°的两个等腰三角形相似;②有一个角为100°的两个等腰三角形相似;③有一个锐角相等的两个直角三角形相似;④两个等边三角形相似.其中正确的是______(填序号);
(2)如图2,已知AB∥CD,AD与BC相交于点O,试说明△ABO∽△DCO;
(3)如图3,在平行四边形ABCD中,E是DC上一点,连接AE.F为AE上一点,且∠BFE=∠C,求证:△ABF∽△EAD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与x轴交于点A(-1,0),点B(3,0),与y轴正半轴交于点C.
与x轴交于点A(-1,0),点B(3,0),与y轴正半轴交于点C.
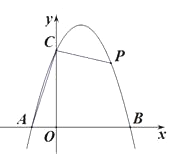
(1)抛物线的解析式为________;
(2)P为抛物线上一点,连结AC,PC,若∠PCO=3∠ACO,点P的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(x1,y1)、B(x2,y2)在二次函数y=x2+mx+n的图象上,当x1=1、x2=3时,y1=y2.
(1)①求m;②若抛物线与x轴只有一个公共点,求n的值.
(2)若P(a,b1),Q(3,b2)是函数图象上的两点,且b1>b2,求实数a的取值范围.
(3)若对于任意实数x1、x2都有y1+y2≥2,求n的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
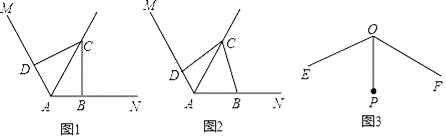
【题目】已知∠MAN=120°,点C是∠MAN的平分线AQ上的一个定点,点B,D分别在AN,AM上,连接BD.
【发现】
(1)如图1,若∠ABC=∠ADC=90°,则∠BCD= °,△CBD是 三角形;
【探索】
(2)如图2,若∠ABC+∠ADC=180°,请判断△CBD的形状,并证明你的结论;
【应用】
(3)如图3,已知∠EOF=120°,OP平分∠EOF,且OP=1,若点G,H分别在射线OE,OF上,且△PGH为等边三角形,则满足上述条件的△PGH的个数一共有 .(只填序号)
①2个②3个③4个④4个以上
查看答案和解析>>
科目:初中数学 来源: 题型:
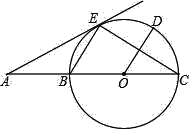
【题目】如图,BC是⊙O的直径,D、E是⊙O上的两点,且弧CD=DE,连接EB、DO.
(1)求证:EB∥DO;
(2)连接EC,在∠CEB的外部作∠BEA=∠C,直线EA交CB的延长线于A,求证:直线EA是⊙O的切线;
(3)若EA=2,AB=1,求⊙O的半径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com