
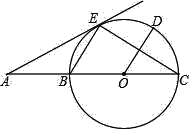
【题目】如图,BC是⊙O的直径,D、E是⊙O上的两点,且弧CD=DE,连接EB、DO.
(1)求证:EB∥DO;
(2)连接EC,在∠CEB的外部作∠BEA=∠C,直线EA交CB的延长线于A,求证:直线EA是⊙O的切线;
(3)若EA=2,AB=1,求⊙O的半径长.
【答案】(1)见解析;(2)见解析;(3)⊙O半径长为![]() .
.
【解析】
(1)由垂径定理得:OD⊥EC;由圆周角定理,得:BE⊥EC;由此可证得EB∥DO;
(2)连接OE,证得∠OEA=90°即可;
(3)根据AE2=ABAC,即可求得AC长,进而求得⊙O的半径长.
(1)∵弧CD=DE,
∴OD⊥EC,
∵BC是⊙O的直径,
∴∠BEC=90°,
∴BE⊥EC,
∴EB∥DO;
(2)连接OE,
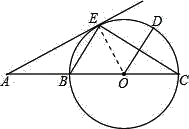
∵OC=OE,
∴∠C=∠OEC,
∵∠BEA=∠C,
∴∠BEA=∠OEC,
∵∠CEO+∠BEO=90°,
∴∠BEA+∠BEO=90°,即∠OEA=90°,
∴直线EA是⊙O的切线;
(3)∵AE是切线,AC是割线,
∴由切割线定理知:AE2=ABAC,
∴AC=AE2÷AB=4,
∴BC=AC﹣AB=3,
∴⊙O半径长为![]() .
.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() (a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.
(a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.

(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点B的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且△MAC为等腰三角形,请直接写出所有符合条件的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.

(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图2.
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:到一个三角形三个顶点的距离相等的点叫做该三角形的外心.
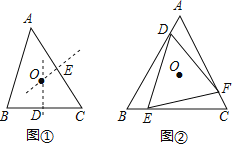
(1)如图①,小海同学在作△ABC的外心时,只作出两边BC,AC的垂直平分线得到交点O,就认定点O是△ABC的外心,你觉得有道理吗?为什么?
(2)如图②,在等边三角形ABC的三边上,分别取点D,E,F,使AD=BE=CF,连接DE,EF,DF,得到△DEF.若点O为△ABC的外心,求证:点O也是△DEF的外心.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:“直角三角形如果有一个角等于![]() ,那么这个角所对的边等于斜边的一半”,即“在
,那么这个角所对的边等于斜边的一半”,即“在![]() 中,
中,![]() ,则
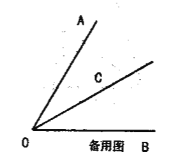
,则![]() ”.利用以上知识解决下列问题:如图,已知
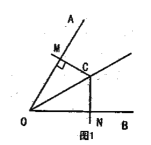
”.利用以上知识解决下列问题:如图,已知![]() 是
是![]() 的平分线上一点.
的平分线上一点.
(1)若![]() 与射线
与射线![]() 分别相交于点
分别相交于点![]() ,且
,且![]() .
.
①如图1,当![]() 时,求证:
时,求证: ![]() ;
;
②当![]() 时,求
时,求![]() 的值.
的值.
(2)若![]() 与射线
与射线![]() 的反向延长线、射线
的反向延长线、射线![]() 分别相交于点
分别相交于点![]() ,且
,且![]() ,请你直接写出线段
,请你直接写出线段![]() 三者之间的等量关系.
三者之间的等量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
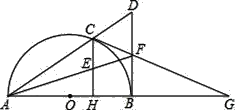
【题目】如图,已知:C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,E为CH中点,连接AE并延长交BD于点F,直线CF交直线AB于点G.
(1)求证:点F是BD中点;
(2)求证:CG是⊙O的切线;
(3)若FB=FE=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙M交x轴于B、C两点,交y轴于A,点M的纵坐标为2.B(﹣3![]() ,O),C(
,O),C(![]() ,O).
,O).
(1)求⊙M的半径;
(2)若CE⊥AB于H,交y轴于F,求证:EH=FH.
(3)在(2)的条件下求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B是反比例函数y=![]() (k≠0)图象上的两点,延长线段AB交y 轴于点C,且点B为线段AC中点,过点A作AD⊥x轴子点D,点E 为线段OD的三等分点,且OE<DE.连接AE、BE,若S△ABE=7,则k的值为( )
(k≠0)图象上的两点,延长线段AB交y 轴于点C,且点B为线段AC中点,过点A作AD⊥x轴子点D,点E 为线段OD的三等分点,且OE<DE.连接AE、BE,若S△ABE=7,则k的值为( )

A. ﹣12 B. ﹣10 C. ﹣9 D. ﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
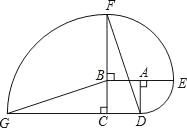
【题目】如图,四边形ABCD是边长为2的正方形,以点A,B,C为圆心作圆,分别交BA,CB,DC的延长线于点E,F,G.
(1)求点D沿三条圆弧运动到点G所经过的路线长;
(2)判断线段GB与DF的长度关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com