
【题目】如图,点A、B是反比例函数y=![]() (k≠0)图象上的两点,延长线段AB交y 轴于点C,且点B为线段AC中点,过点A作AD⊥x轴子点D,点E 为线段OD的三等分点,且OE<DE.连接AE、BE,若S△ABE=7,则k的值为( )
(k≠0)图象上的两点,延长线段AB交y 轴于点C,且点B为线段AC中点,过点A作AD⊥x轴子点D,点E 为线段OD的三等分点,且OE<DE.连接AE、BE,若S△ABE=7,则k的值为( )

A. ﹣12 B. ﹣10 C. ﹣9 D. ﹣6
【答案】A
【解析】
设A(m,![]() ),C(0,n),则D(m,0),E(
),C(0,n),则D(m,0),E(![]() m,0),由AB=BC,推出B(
m,0),由AB=BC,推出B(![]() ,
,![]() ),根据点B在y=
),根据点B在y=![]() 上,推出
上,推出![]()
![]() =k,可得mn=3k,连接EC,OA.因为AB=BC,推出S△AEC=2S△AEB=14,根据S△AEC=S△AEO+S△ACO-S△ECO,构建方程即可解决问题.
=k,可得mn=3k,连接EC,OA.因为AB=BC,推出S△AEC=2S△AEB=14,根据S△AEC=S△AEO+S△ACO-S△ECO,构建方程即可解决问题.
解:设A(m,![]() ),C(0,n),则D(m,0),E(
),C(0,n),则D(m,0),E(![]() m,0),
m,0),
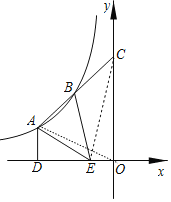
∵AB=BC,
∴B(![]() ,
,![]() ),
),
∵点B在y=![]() 上,
上,
∴![]()
![]() =k,
=k,
∴k+mn=4k,
∴mn=3k,
连接EC,OA.
∵AB=BC,
∴S△AEC=2S△AEB=14,
∵S△AEC=S△AEO+S△ACO-S△ECO,
∴14=![]() (-
(-![]() m)
m)![]() +
+![]() n(-m)-
n(-m)-![]() (-
(-![]() m)n,
m)n,
∴14=-![]() k-
k-![]() +
+![]() ,
,
∴k=-12.
故选:A.


科目:初中数学 来源: 题型:
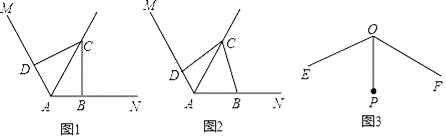
【题目】已知∠MAN=120°,点C是∠MAN的平分线AQ上的一个定点,点B,D分别在AN,AM上,连接BD.
【发现】
(1)如图1,若∠ABC=∠ADC=90°,则∠BCD= °,△CBD是 三角形;
【探索】
(2)如图2,若∠ABC+∠ADC=180°,请判断△CBD的形状,并证明你的结论;
【应用】
(3)如图3,已知∠EOF=120°,OP平分∠EOF,且OP=1,若点G,H分别在射线OE,OF上,且△PGH为等边三角形,则满足上述条件的△PGH的个数一共有 .(只填序号)
①2个②3个③4个④4个以上
查看答案和解析>>
科目:初中数学 来源: 题型:
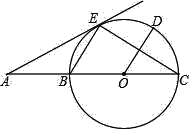
【题目】如图,BC是⊙O的直径,D、E是⊙O上的两点,且弧CD=DE,连接EB、DO.
(1)求证:EB∥DO;
(2)连接EC,在∠CEB的外部作∠BEA=∠C,直线EA交CB的延长线于A,求证:直线EA是⊙O的切线;
(3)若EA=2,AB=1,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组在讨论“变化的三角形”时,知道大三角形与小三角形是位似图形(如图所示),则小三角形上的顶点(a,b)对应于大三角形上的顶点 ( )

A. (-2a,-2b) B. (2a,2b) C. (-2b,-2a) D. (-2a,-b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,两个不全等的等腰直角三角形![]() 和
和![]() 叠放在一起,并且有公共的直角顶点
叠放在一起,并且有公共的直角顶点![]() .
.
(1)在图1中,你发现线段![]() 的数量关系是______.直线
的数量关系是______.直线![]() 相交成_____度角.
相交成_____度角.
(2)将图1中![]() 绕点
绕点![]() 顺时针旋转90°,连接
顺时针旋转90°,连接![]() 得到图2,这时(1)中的两个结论是否成立?请作出判断说明理由.
得到图2,这时(1)中的两个结论是否成立?请作出判断说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy内,函数y=![]() x的图象与反比例函数y=
x的图象与反比例函数y=![]() (k≠0)图象有公共点A,点A的坐标为(4,a),AB⊥x轴,垂足为点B.
(k≠0)图象有公共点A,点A的坐标为(4,a),AB⊥x轴,垂足为点B.
(1)求反比例函数的解析式;
(2)点C是第一象限内直线OA上一点,过点C作直线CD∥AB,与反比例函数y=![]() (k≠0)的图象交于点D,且点C在点D的上方,CD=
(k≠0)的图象交于点D,且点C在点D的上方,CD=![]() AB,求点D的坐标.
AB,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动我县“三进校园”活动的广泛开展,引导学生走向操场,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据相关信息,解答下列问题:

(1)本次接受随机抽样调查的学生人数为 ,图①中![]() 的值为 ;
的值为 ;
(2)本次调查获取的样本数据的众数为 ,中位数为 ;
(3)根据样本数据,若学校计划购买![]() 双运动鞋,建议购买
双运动鞋,建议购买![]() 号运动鞋 双.
号运动鞋 双.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人参加射击比赛,两人成绩如图所示.
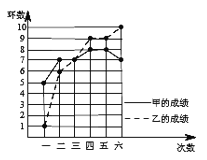
(1)填表:
平均数 | 方差 | 中位数 | 众数 | |
甲 | 7 | 1 | 7 | |
乙 | 9 |
(2)只看平均数和方差,成绩更好的是 .(填“甲”或“乙”)
(3)仅就折线图上两人射击命中环数的走势看,更有潜力的是 .(填“甲”或“乙”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com