
【题目】为了推动我县“三进校园”活动的广泛开展,引导学生走向操场,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据相关信息,解答下列问题:

(1)本次接受随机抽样调查的学生人数为 ,图①中![]() 的值为 ;
的值为 ;
(2)本次调查获取的样本数据的众数为 ,中位数为 ;
(3)根据样本数据,若学校计划购买![]() 双运动鞋,建议购买
双运动鞋,建议购买![]() 号运动鞋 双.
号运动鞋 双.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)60.
;(3)60.
【解析】
(1)根据条形统计图求出总人数即可;由扇形统计图以及单位1,求出m的值即可;
(2)找出出现次数最多的即为众数,将数据按照从小到大顺序排列,求出中位数即可;
(3)根据题意列出算式,计算即可得到结果.
解:(1)本次接受随机抽样调查的学生人数为6+12+10+8+4=40,
图①中m的值为10030252010=15;
(2)∵在这组样本数据中,35出现了12次,出现次数最多,
∴这组样本数据的众数为35,
∵将这组样本数据从小到大的顺序排列,其中处于中间的两个数都为36,
∴中位数为![]() (36+36)=36;
(36+36)=36;
(3)∵在40名学生中,鞋号为35的学生人数比例为30%,
∴由样本数据,估计学校各年级中学生鞋号为35的人数比例约为30%,
则计划购买200双运动鞋中35号的鞋有200×30%=60双.
故答案为:(1)40,15;(2)35,36;(3)60.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】正方形网格中,每个小格的顶点叫做格点.当所作正方形边上的点刚好在格点上的点称为整点.如图中![]() 四条边上的整点共有
四条边上的整点共有![]() 个;
个;![]() 四条边上的整点共有
四条边上的整点共有![]() 个.请你观察图中正方形
个.请你观察图中正方形![]() 四条边上的整点的个数…按此规律,推算出正方形
四条边上的整点的个数…按此规律,推算出正方形![]() 四条边上的整点共有________个.
四条边上的整点共有________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某广告公司设计一幅周长为16米的矩形广告牌,广告设计费为每平方米2000元.设矩形一边长为x,面积为S平方米.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围;
(2)设计费能达到24000元吗?为什么?
(3)当x是多少米时,设计费最多?最多是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程3x2-(a-3)x-a=0(a>0).
(1)求证:方程总有两个不相等的实数根;
(2)若方程有一个根大于2,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次平移,每次移动一个单位,得到点![]() …..那么点
…..那么点![]() 的坐标为________.
的坐标为________.
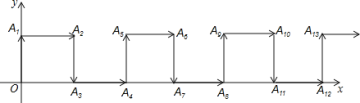
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的顶点A、B在x轴上,顶点D在反比例函数y=![]() (k>0)的图象上,CA的延长线交y轴于点E,连接BE.若S△ABE=2,则k的值为( )
(k>0)的图象上,CA的延长线交y轴于点E,连接BE.若S△ABE=2,则k的值为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个n位自然数![]() 能被x0整除,依次轮换个位数字得到的新数
能被x0整除,依次轮换个位数字得到的新数![]() 能被x0+1整除,再依次轮换个位数字得到的新数
能被x0+1整除,再依次轮换个位数字得到的新数![]() 能被x0+2整除,按此规律轮换后,
能被x0+2整除,按此规律轮换后,![]() 能被x0+3整除,…,
能被x0+3整除,…,![]() 能被x0+n﹣1整除,则称这个n位数
能被x0+n﹣1整除,则称这个n位数![]() 是x0的一个“轮换数”.
是x0的一个“轮换数”.
例如:60能被5整除,06能被6整除,则称两位数60是5的一个“轮换数”;
再如:324能被2整除,243能被3整除,432能被4整除,则称三位数324是2个一个“轮换数”.
(1)若一个两位自然数的个位数字是十位数字的2倍,求证这个两位自然数一定是“轮换数”.
(2)若三位自然数![]() 是3的一个“轮换数”,其中a=2,求这个三位自然数
是3的一个“轮换数”,其中a=2,求这个三位自然数![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com