
【题目】有一个n位自然数![]() 能被x0整除,依次轮换个位数字得到的新数
能被x0整除,依次轮换个位数字得到的新数![]() 能被x0+1整除,再依次轮换个位数字得到的新数
能被x0+1整除,再依次轮换个位数字得到的新数![]() 能被x0+2整除,按此规律轮换后,
能被x0+2整除,按此规律轮换后,![]() 能被x0+3整除,…,
能被x0+3整除,…,![]() 能被x0+n﹣1整除,则称这个n位数
能被x0+n﹣1整除,则称这个n位数![]() 是x0的一个“轮换数”.
是x0的一个“轮换数”.
例如:60能被5整除,06能被6整除,则称两位数60是5的一个“轮换数”;
再如:324能被2整除,243能被3整除,432能被4整除,则称三位数324是2个一个“轮换数”.
(1)若一个两位自然数的个位数字是十位数字的2倍,求证这个两位自然数一定是“轮换数”.
(2)若三位自然数![]() 是3的一个“轮换数”,其中a=2,求这个三位自然数
是3的一个“轮换数”,其中a=2,求这个三位自然数![]() .
.
【答案】(1)见解析;(2) 201,207,255
【解析】
试题(1)先设出两位自然数的十位数字,表示出这个两位自然数,和轮换两位自然数即可;
(2)先表示出三位自然数和轮换三位自然数,再根据能被5整除,得出b的可能值,进而用4整除,得出c的可能值,最后用能被3整除即可.
试题解析:
(1)设两位自然数的十位数字为x,则个位数字为2x,
∴这个两位自然数是10x+2x=12x,
∴这个两位自然数是12x能被6整除,
∵依次轮换个位数字得到的两位自然数为10×2x+x=21x
∴轮换个位数字得到的两位自然数为21x能被7整除,
∴一个两位自然数的个位数字是十位数字的2倍,这个两位自然数一定是“轮换数”.
(2)∵三位自然数![]() 是3的一个“轮换数”,且a=2,
是3的一个“轮换数”,且a=2,
∴100a+10b+c能被3整除,
即:10b+c+200能被3整除,
第一次轮换得到的三位自然数是100b+10c+a能被4整除,
即100b+10c+2能被4整除,
第二次轮换得到的三位自然数是100c+10a+b能被5整除,
即100c+b+20能被5整除,
∵100c+b+20能被5整除,
∴b+20的个位数字不是0,便是5,
∴b=0或b=5,
当b=0时,
∵100b+10c+2能被4整除,
∴10c+2能被4整除,
∴c只能是1,3,5,7,9;
∴这个三位自然数可能是为201,203,205,207,209,
而203,205,209不能被3整除,
∴这个三位自然数为201,207,
当b=5时,∵100b+10c+2能被4整除,
∴10c+502能被4整除,
∴c只能是1,5,7,9;
∴这个三位自然数可能是为251,255,257,259,
而251,257,259不能被3整除,
∴这个三位自然数为255,
即这个三位自然数为201,207,255.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
【题目】为了推动我县“三进校园”活动的广泛开展,引导学生走向操场,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据相关信息,解答下列问题:

(1)本次接受随机抽样调查的学生人数为 ,图①中![]() 的值为 ;
的值为 ;
(2)本次调查获取的样本数据的众数为 ,中位数为 ;
(3)根据样本数据,若学校计划购买![]() 双运动鞋,建议购买
双运动鞋,建议购买![]() 号运动鞋 双.
号运动鞋 双.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 A,B,C 的坐标分别是(2,1),(6,1),(3,5),若△A1B1C1 与△ABC 关于x 轴对称
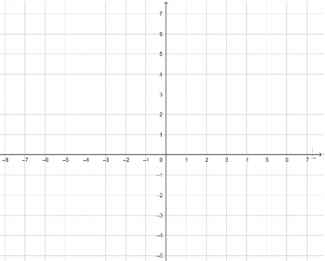
(1)在平面直角坐标系中画出△A1B1C1,并写出 A1,B1,C1 三个点的坐标
(2)求出△A1B1C1的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
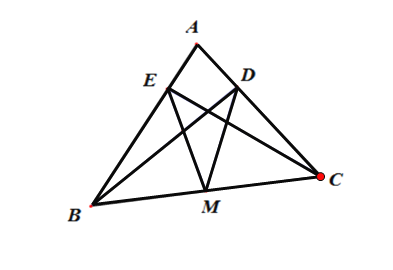
【题目】(1)已知:如图,在△ABC中,BD⊥AC于D,CE⊥AB于E,M是BC的中点.求证:MD=ME.
(2)已知:如图,O是△ABC内任意一点,且满足∠1=∠2,OD⊥AC于D, OE⊥AB于E,M是BC的中点。仿照第⑴问的思路,结合三角形中位线定理,平行四边形的性质与判定,求证:MD=ME.
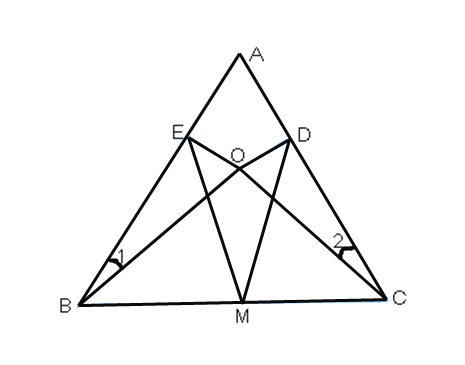
查看答案和解析>>
科目:初中数学 来源: 题型:
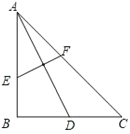
【题目】如图,已知在△ABC中,∠B=90°,AB=BC,AD是BC边上的中线,EF是AD的垂直平分线,交AB于点E,交AC于点F,则AE:BE的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在宽20米,长32米的矩形耕地上,修筑同样宽的三条路(两条纵向,一条横向,并且横向与纵向互相垂直),把这块耕地分成大小相等的六块试验田,要使试验田的面积是570平方米,问道路应该多宽?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条东西走向的笔直公路,点A、B表示公路北侧间隔150米的两棵树所在的位置,点C表示电视塔所在的位置.小王在公路PQ南侧直线行走,当他到达点P的位置时,观察树A恰好挡住电视塔,即点P、A、C在一条直线上,当他继续走180米到达点Q的位置时,以同样方法观察电视塔,观察树B也恰好挡住电视塔.假设公路两侧AB∥PQ,且公路的宽为60米,求电视塔C到公路南侧PQ的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣(x﹣h)2(h为常数),当自变量x的值满足2≤x≤5时,与其对应的函数值y的最大值为﹣1,则h的值为( )
A. 3或6 B. 1或6 C. 1或3 D. 4或6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com