
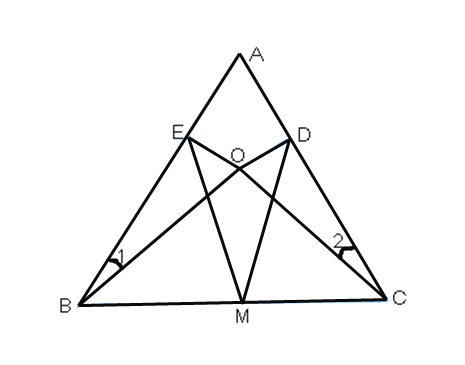
【题目】(1)已知:如图,在△ABC中,BD⊥AC于D,CE⊥AB于E,M是BC的中点.求证:MD=ME.
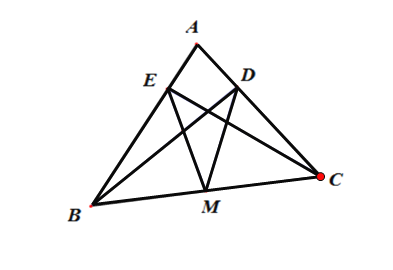
(2)已知:如图,O是△ABC内任意一点,且满足∠1=∠2,OD⊥AC于D, OE⊥AB于E,M是BC的中点。仿照第⑴问的思路,结合三角形中位线定理,平行四边形的性质与判定,求证:MD=ME.
【答案】(1)见详解;(2)见详解.
【解析】
(1)由BD⊥AC于D,CE⊥AB于E,则△BCD,△BCE是直角三角形,由点M是BC中点,即可得到EM=DM=![]() ;
;
(2)分别取BO中点F、CO中点G,连接EF、FM、DG、GM,由直角三角形斜边上的中线等于斜边的一半,得到EF=BF=OF=![]() OB,DG=OG=CG=
OB,DG=OG=CG=![]() OC,然后根据∠1=∠2,得到∠EFO=∠DGO;由三角形中位线定理,得到四边形OFMG是平行四边形,则∠OFM=∠OGM,从而得到∠EFM=∠DGM,利用SAS证明△EFM≌△MGD,即可得到结论成立.
OC,然后根据∠1=∠2,得到∠EFO=∠DGO;由三角形中位线定理,得到四边形OFMG是平行四边形,则∠OFM=∠OGM,从而得到∠EFM=∠DGM,利用SAS证明△EFM≌△MGD,即可得到结论成立.
证明:(1)如图,
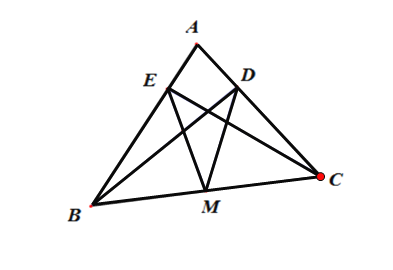
∵BD⊥AC于D,CE⊥AB于E,
∴△BCD,△BCE是直角三角形,
∵点M是BC中点,
∴ME,MD分别是直角三角形△BCE和△BCD的中线,
∴EM=DM=![]() ;
;
(2)如图,分别取BO中点F、CO中点G,连接EF、FM、DG、GM,
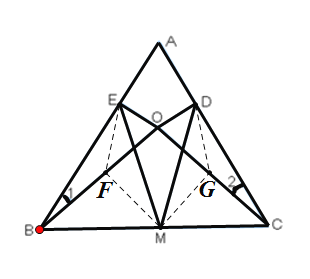
∵OD⊥AC于D,OE⊥AB于E,
∴△OBE、△OCD是直角三角形,
∵点F为OB中点,点G为OC中点,
∴EF=BF=OF=![]() OB,DG=OG=CG=
OB,DG=OG=CG=![]() OC,
OC,
∴∠1=∠BEF,∠2=∠CDG,
∴∠EFO=2∠1,∠DGO=2∠2,
∵∠1=∠2,
∴∠EFO=∠DGO,
∵点M是BC的中点,
∴FM和GM都是△OBC的中位线,
∴FM=![]() OC=OG=DG,GM=
OC=OG=DG,GM=![]() OB=OF=EF,
OB=OF=EF,
∴四边形OFMG是平行四边形,
∴∠OFM=∠OGM,
∴∠EFO+∠OFM=∠DGO+∠OGM,
即∠EFM=∠DGM,
∵FM=DG,EF=MG,
∴△EFM≌△MGD(SAS),
∴EM=MD.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的方程3x2-(a-3)x-a=0(a>0).
(1)求证:方程总有两个不相等的实数根;
(2)若方程有一个根大于2,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的顶点A、B在x轴上,顶点D在反比例函数y=![]() (k>0)的图象上,CA的延长线交y轴于点E,连接BE.若S△ABE=2,则k的值为( )
(k>0)的图象上,CA的延长线交y轴于点E,连接BE.若S△ABE=2,则k的值为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0),下列结论:①ab<0,②b2>4,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0.其中正确结论是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行了“文明在我身边”摄影比赛.已知每幅参赛作品成绩记为x分(60≤x<100).校方从600幅参赛作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.
分数段 | 频数 | 频率 |
60≤x<70 | 18 | 0.36 |
70≤x<80 | 17 | c |
80≤x<90 | a | 0.24 |
90≤x<100 | b | 0.06 |
合计 | 1 |

根据以上信息解答下列问题:
(1)统计表中c的值为________;样本成绩的中位数落在分数段________中;
(2)补全频数直方图;
(3)若80分以上(含80分)的作品将被组织展评,试估计全校被展评的作品数量是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲乙两艘巡逻艇立即从相距13海里的A、B两基地前去拦截,6分钟后同时到达C地成功将其拦截,已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,航向为北偏西40°,则甲巡逻艇航向为北偏东________°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个n位自然数![]() 能被x0整除,依次轮换个位数字得到的新数
能被x0整除,依次轮换个位数字得到的新数![]() 能被x0+1整除,再依次轮换个位数字得到的新数
能被x0+1整除,再依次轮换个位数字得到的新数![]() 能被x0+2整除,按此规律轮换后,
能被x0+2整除,按此规律轮换后,![]() 能被x0+3整除,…,
能被x0+3整除,…,![]() 能被x0+n﹣1整除,则称这个n位数
能被x0+n﹣1整除,则称这个n位数![]() 是x0的一个“轮换数”.
是x0的一个“轮换数”.
例如:60能被5整除,06能被6整除,则称两位数60是5的一个“轮换数”;
再如:324能被2整除,243能被3整除,432能被4整除,则称三位数324是2个一个“轮换数”.
(1)若一个两位自然数的个位数字是十位数字的2倍,求证这个两位自然数一定是“轮换数”.
(2)若三位自然数![]() 是3的一个“轮换数”,其中a=2,求这个三位自然数
是3的一个“轮换数”,其中a=2,求这个三位自然数![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
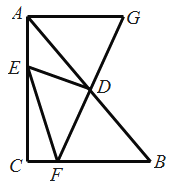
【题目】如图,在![]() 中,D是边AB的中点,E是边AC上一动点,连接DE,过点D作DF⊥DE交边BC于点F(点F与点B、C不重合),延长FD到点G,使
中,D是边AB的中点,E是边AC上一动点,连接DE,过点D作DF⊥DE交边BC于点F(点F与点B、C不重合),延长FD到点G,使![]() ,连接EF、AG,已知
,连接EF、AG,已知![]() ,
,![]() ,
,![]() .
.
(1)试说明![]() ;
;
(2)请你连接EG,设![]() ,
,![]() ,求y关于x的函数关系式;
,求y关于x的函数关系式;
(3)当![]() 是以BF为腰的等腰三角形时,直接写出AE的长,不必说明理由.
是以BF为腰的等腰三角形时,直接写出AE的长,不必说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com