
【题目】如图,正方形ABCD的顶点A、B在x轴上,顶点D在反比例函数y=![]() (k>0)的图象上,CA的延长线交y轴于点E,连接BE.若S△ABE=2,则k的值为( )
(k>0)的图象上,CA的延长线交y轴于点E,连接BE.若S△ABE=2,则k的值为( )

A. 1 B. 2 C. 3 D. 4
科目:初中数学 来源: 题型:
【题目】如图1摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM、ME.
(1)试猜想DM与ME的关系,并证明你的结论.
(2)若将图1中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为______.
(3)如图2摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的点,则DM和ME的关系为______,并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动我县“三进校园”活动的广泛开展,引导学生走向操场,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据相关信息,解答下列问题:

(1)本次接受随机抽样调查的学生人数为 ,图①中![]() 的值为 ;
的值为 ;
(2)本次调查获取的样本数据的众数为 ,中位数为 ;
(3)根据样本数据,若学校计划购买![]() 双运动鞋,建议购买
双运动鞋,建议购买![]() 号运动鞋 双.
号运动鞋 双.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b与x轴y轴分别交于点E、F,点E的坐标为(8,0),点F的坐标为(0,6),点A的坐标为(6,0).
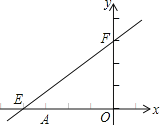
(1)求k和b的值;
(2)若点P(x,y)是第二象限内的直线上的一个动点,在点P的运动过程中,求出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当点P运动到什么位置时,△OPA的面积为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在双曲线y=![]() (x>0)上,点C在双曲线y=
(x>0)上,点C在双曲线y=![]() (x>0)上,若AC∥y轴,BC∥x轴,且AC=BC,则AB等于( )
(x>0)上,若AC∥y轴,BC∥x轴,且AC=BC,则AB等于( )

A. ![]() B. 2
B. 2![]() C. 4 D. 3
C. 4 D. 3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列各题
(1)解方程:﹣x2+4x﹣3=0.
(2)已知一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A(2,m),B(﹣1、n),求一次函数的解析式.
的图象交于点A(2,m),B(﹣1、n),求一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 A,B,C 的坐标分别是(2,1),(6,1),(3,5),若△A1B1C1 与△ABC 关于x 轴对称
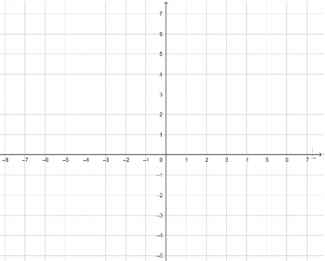
(1)在平面直角坐标系中画出△A1B1C1,并写出 A1,B1,C1 三个点的坐标
(2)求出△A1B1C1的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知:如图,在△ABC中,BD⊥AC于D,CE⊥AB于E,M是BC的中点.求证:MD=ME.
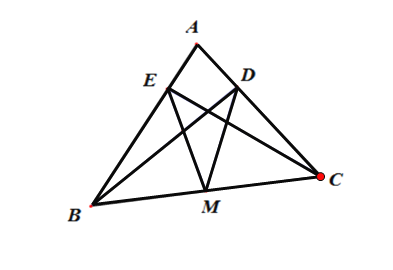
(2)已知:如图,O是△ABC内任意一点,且满足∠1=∠2,OD⊥AC于D, OE⊥AB于E,M是BC的中点。仿照第⑴问的思路,结合三角形中位线定理,平行四边形的性质与判定,求证:MD=ME.
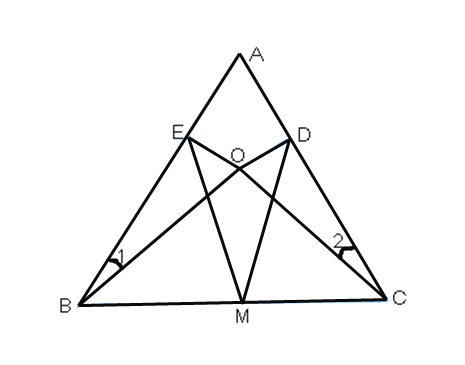
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条东西走向的笔直公路,点A、B表示公路北侧间隔150米的两棵树所在的位置,点C表示电视塔所在的位置.小王在公路PQ南侧直线行走,当他到达点P的位置时,观察树A恰好挡住电视塔,即点P、A、C在一条直线上,当他继续走180米到达点Q的位置时,以同样方法观察电视塔,观察树B也恰好挡住电视塔.假设公路两侧AB∥PQ,且公路的宽为60米,求电视塔C到公路南侧PQ的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com