
【题目】如图所示,⊙O半径为2,弦BD=2![]() ,A为弧BD的中点,E为弦AC的中点,且在BD上,求四边形ABCD的面积.
,A为弧BD的中点,E为弦AC的中点,且在BD上,求四边形ABCD的面积.

【答案】![]() .
.
【解析】
由A是弧BD的中点,根据垂径定理,可知OF⊥BD,且BF=DF=![]() ×BD×AF=
×BD×AF=![]() ,而E是AC中点,会出现等底同高的三角形,因而有S四边形=2S△ABD=2
,而E是AC中点,会出现等底同高的三角形,因而有S四边形=2S△ABD=2![]() .
.
连结OA交BD于点F,连接OB.

∵OA在直径上且点A是BD中点,
∴OA⊥BD, BF=DF=![]() .
.
在Rt△BOF中,由勾股定理得OF2=OB2-BF2,
OF=![]()
![]()
![]()
![]() =
=![]() .
.
∵点E 是AC中点,
∴AE=CE.
又∵△ADE和△CDE同高,
∴S△CDE=S△ADE,
同理S△CBE =S△ABE,
∴S△BCD =S△CDE +S△CBE =S△ADE +S△ABE =S△ABD =![]() ,
,
∴S四边形ABCD=S△ABD +S△BCD =2![]() .
.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
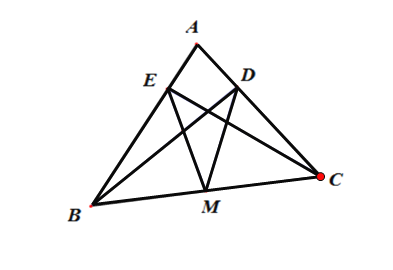
【题目】(1)已知:如图,在△ABC中,BD⊥AC于D,CE⊥AB于E,M是BC的中点.求证:MD=ME.
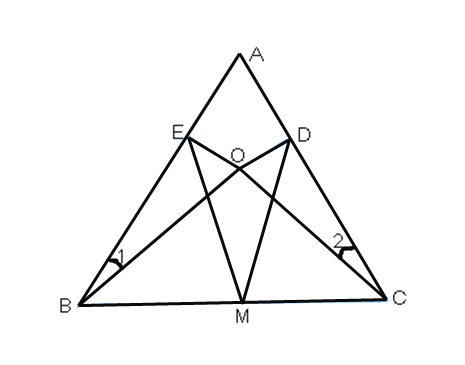
(2)已知:如图,O是△ABC内任意一点,且满足∠1=∠2,OD⊥AC于D, OE⊥AB于E,M是BC的中点。仿照第⑴问的思路,结合三角形中位线定理,平行四边形的性质与判定,求证:MD=ME.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条东西走向的笔直公路,点A、B表示公路北侧间隔150米的两棵树所在的位置,点C表示电视塔所在的位置.小王在公路PQ南侧直线行走,当他到达点P的位置时,观察树A恰好挡住电视塔,即点P、A、C在一条直线上,当他继续走180米到达点Q的位置时,以同样方法观察电视塔,观察树B也恰好挡住电视塔.假设公路两侧AB∥PQ,且公路的宽为60米,求电视塔C到公路南侧PQ的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点的位置如图所示

(1)请画出△ABC关于y轴对称的△A′B′C′;(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
(2)直接写出A′B′C′三点的坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2x+m﹣2=0有两个实数根,m为正整数,且该方程的根都是整数,则符合条件的所有正整数m的和为( )
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣(x﹣h)2(h为常数),当自变量x的值满足2≤x≤5时,与其对应的函数值y的最大值为﹣1,则h的值为( )
A. 3或6 B. 1或6 C. 1或3 D. 4或6
查看答案和解析>>
科目:初中数学 来源: 题型:
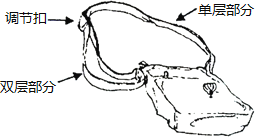
【题目】如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小垣用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:
(1)根据表中数据的规律,补全以下表格,并求出y关于x的函数表达式;
单层部分的长度x(cm) | … | 4 | 6 | 8 | 10 | … | 150 |
双层部分的长度y(cm) | … | 73 | 72 | 71 | ______ | … | ______ |
(2)根据小垣的身高和习惯,挎带的长度为120cm时,背起来正合适,请求出此时单层部分的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求.商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com