
【题目】如图,⊙M交x轴于B、C两点,交y轴于A,点M的纵坐标为2.B(﹣3![]() ,O),C(
,O),C(![]() ,O).
,O).
(1)求⊙M的半径;
(2)若CE⊥AB于H,交y轴于F,求证:EH=FH.
(3)在(2)的条件下求AF的长.

【答案】(1)4;(2)见解析;(3)4.
【解析】
(1)过M作MT⊥BC于T连BM,由垂径定理可求出BT的长,再由勾股定理即可求出BM的长;
(2)连接AE,由圆周角定理可得出∠AEC=∠ABC,再由AAS定理得出△AEH≌△AFH,进而可得出结论;
(3)先由(1)中△BMT的边长确定出∠BMT的度数,再由直角三角形的性质可求出CG的长,由平行四边形的判定定理判断出四边形AFCG为平行四边形,进而可求出答案.
(1)如图(一),过M作MT⊥BC于T连BM,
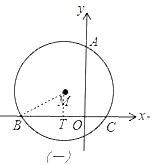
∵BC是⊙O的一条弦,MT是垂直于BC的直径,
∴BT=TC=![]() BC=2
BC=2![]() ,
,
∴BM=![]() =4;
=4;
(2)如图(二),连接AE,则∠AEC=∠ABC,
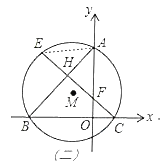
∵CE⊥AB,
∴∠HBC+∠BCH=90°
在△COF中,
∵∠OFC+∠OCF=90°,
∴∠HBC=∠OFC=∠AFH,
在△AEH和△AFH中,
∵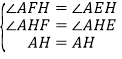 ,
,
∴△AEH≌△AFH(AAS),
∴EH=FH;
(3)由(1)易知,∠BMT=∠BAC=60°,
作直径BG,连CG,则∠BGC=∠BAC=60°,
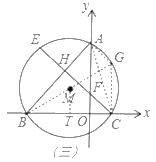
∵⊙O的半径为4,
∴CG=4,
连AG,
∵∠BCG=90°,
∴CG⊥x轴,
∴CG∥AF,
∵∠BAG=90°,
∴AG⊥AB,
∵CE⊥AB,
∴AG∥CE,
∴四边形AFCG为口,
∴AF=CG=4.


科目:初中数学 来源: 题型:
【题目】已知:如图,点P在线段AB外,且PA=PB,求证:点P在线段AB的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )

A. 作∠APB的平分线PC交AB于点C
B. 过点P作PC⊥AB于点C且AC=BC
C. 取AB中点C,连接PC
D. 过点P作PC⊥AB,垂足为C
查看答案和解析>>
科目:初中数学 来源: 题型:
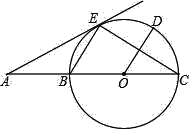
【题目】如图,BC是⊙O的直径,D、E是⊙O上的两点,且弧CD=DE,连接EB、DO.
(1)求证:EB∥DO;
(2)连接EC,在∠CEB的外部作∠BEA=∠C,直线EA交CB的延长线于A,求证:直线EA是⊙O的切线;
(3)若EA=2,AB=1,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由6个大小相同的小正方形组成的方格.
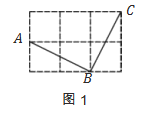
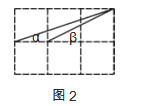
(1)如图1,A、B、C是三个格点,判断AB与BC的位置关系,并说明理由;
(2)如图2,直接写出∠α+∠β的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组在讨论“变化的三角形”时,知道大三角形与小三角形是位似图形(如图所示),则小三角形上的顶点(a,b)对应于大三角形上的顶点 ( )

A. (-2a,-2b) B. (2a,2b) C. (-2b,-2a) D. (-2a,-b)
查看答案和解析>>
科目:初中数学 来源: 题型:
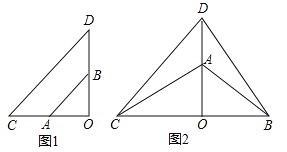
【题目】如图1,两个不全等的等腰直角三角形![]() 和
和![]() 叠放在一起,并且有公共的直角顶点
叠放在一起,并且有公共的直角顶点![]() .
.
(1)在图1中,你发现线段![]() 的数量关系是______.直线
的数量关系是______.直线![]() 相交成_____度角.
相交成_____度角.
(2)将图1中![]() 绕点
绕点![]() 顺时针旋转90°,连接
顺时针旋转90°,连接![]() 得到图2,这时(1)中的两个结论是否成立?请作出判断说明理由.
得到图2,这时(1)中的两个结论是否成立?请作出判断说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动我县“三进校园”活动的广泛开展,引导学生走向操场,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据相关信息,解答下列问题:

(1)本次接受随机抽样调查的学生人数为 ,图①中![]() 的值为 ;
的值为 ;
(2)本次调查获取的样本数据的众数为 ,中位数为 ;
(3)根据样本数据,若学校计划购买![]() 双运动鞋,建议购买
双运动鞋,建议购买![]() 号运动鞋 双.
号运动鞋 双.
查看答案和解析>>
科目:初中数学 来源: 题型:
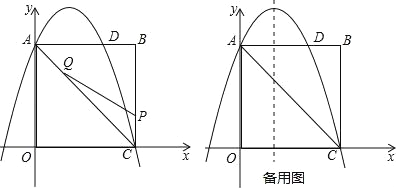
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com