
【题目】如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y= ![]() +bx+c的顶点,则抛物线y=
+bx+c的顶点,则抛物线y= ![]() +bx+c与直线y=1交点的个数是( )
+bx+c与直线y=1交点的个数是( ) 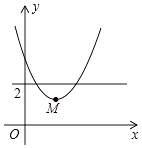
A.0个或1个
B.0个或2个
C.1个或2个
D.0个、1个或2个
【答案】D
【解析】解:由抛物线y=x2+bx+c的图象可知,该抛物线与x轴没有交点, 即:△<0,
则:b2﹣4c<0,
又点M是直线y=2与x轴之间的一个动点,点M的坐标为:(﹣ ![]() ,
, ![]() ),
),
所以,0< ![]() <2,即:﹣8<b2﹣4c<0,
<2,即:﹣8<b2﹣4c<0,
令y=x2+bx+c﹣1,则要求方程x2+bx+c=1的解得个数,只需判定抛物线y=x2+bx+c﹣1与x轴有无交点及交点的个数即可.
又因为,△=b2﹣4ac=b2﹣4(c﹣1)=b2﹣4c+4,
所以,﹣4<b2﹣4c+4<4,
即:①当﹣4<b2﹣4c+4<0时,抛物线y=x2+bx+c﹣1与x轴没有交点;②b2﹣4c+4=0时,抛物线y=x2+bx+c﹣1与x轴有一个交点;③0<b2﹣4c+4<4时,抛物线y=x2+bx+c﹣1与x轴有两个交点.
故选:D.
【考点精析】根据题目的已知条件,利用二次函数的性质的相关知识可以得到问题的答案,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】小明早晨从家里出发匀速步行去上学,小明的妈妈在小明出发后10分钟,发现小明的数学课本没带,于是她带上课本立即匀速骑车按小明上学的路线追赶小明,结果与小明同时到达学校.已知小明在整个上学途中,他出发后t分钟时,他所在的位置与家的距离为s千米,且s与t之间的函数关系的图象如图中的折线段OA﹣AB所示. 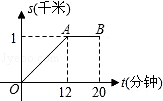
(1)试求折线段OA﹣AB所对应的函数关系式;
(2)请解释图中线段AB的实际意义;
(3)请在所给的图中画出小明的妈妈在追赶小明的过程中,她所在位置与家的距离s(千米)与小明出发后的时间t(分钟)之间函数关系的图象.(友情提醒:请对画出的图象用数据作适当的标注)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC. 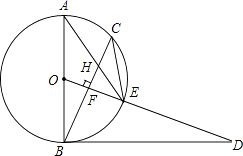
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EHEA;
(3)若⊙O的半径为 ![]() ,sinA=
,sinA= ![]() ,求BH的长.
,求BH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平整的地面上,10个完全相同的棱长为8cm的小正方体堆成一个几何体.
(1)在下面的网格中画出从左面看和从上面看的形状图.

(2)如果在这个几何体的表面(不含底面)喷上黄色的漆,则这个几何体喷漆的面积是多少cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求一个正数的算术平方根,有些数可以直接求得,如![]() ,有些数则不能直接求得,如
,有些数则不能直接求得,如![]() ,但可以通过计算器求. 还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
,但可以通过计算器求. 还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
n | 16 | 0.16 | 0.0016 | 1600 | 160000 | … |
| 4 | 0.4 | 0.04 | 40 | 400 | … |
(1)若![]() ,则
,则![]()
(2)根据你发现的规律,探究下列问题:已知![]() ≈1.435,则:
≈1.435,则:
①![]() ≈ ;
≈ ;
②![]() ≈ ;
≈ ;
(3)根据上述探究过程类比研究一个数的立方根已知![]() ≈1.260,则
≈1.260,则![]() ≈ .
≈ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC. 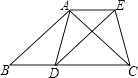
(1)求证:AD=CE;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com