
【题目】已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D.设∠OAC= ![]() °.
°.
(1)如图1,若AB//ON,则①∠ABO的度数是______;②当∠BAD=∠ABD时, ![]() =______;③当∠BAD=∠BDA时,
=______;③当∠BAD=∠BDA时, ![]() =______.
=______.
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
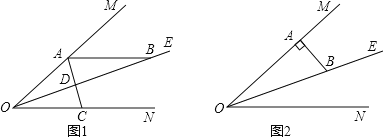
【答案】(1)①20°,②120°,③60°;(2)存在,x=50、20、35或125
【解析】试题分析:(1)①运用平行线的性质以及角平分线的定义,可得①∠ABO的度数;②根据∠ABO、∠BAD的度数以及△AOB的内角和,可得x的值;(2)分两种情况进行讨论:AC在AB左侧,AC在AB右侧,分别根据三角形内角和定理以及直角的度数,可得x的值.
试题解析:如图1,①∵∠MON=36°,OE平分∠MON,
∴∠AOB=∠BON=18,
∵AB∥ON,
∴∠ABO=18;
②当∠BAD=∠ABD时,∠BAD=18°,
∵∠AOB+∠ABO+∠OAB=180°,
∴∠OAC=180°18°×3=126°;
当∠BAD=∠BDA时,∵∠ABO=18°,
∴∠BAD=81°,∠AOB=18°,
∵∠AOB+∠ABO+∠OAB=180°,
∴∠OAC=180°18°18°81°=63°,
故答案为:①18°;②126,63;
(2)如图2,存在这样的x的值,使得△ADB中有两个相等的角。
∵AB⊥OM,∠MON=36,OE平分∠MON,
∴∠AOB=18°,∠ABO=72°,
①当AC在AB左侧时:
若∠BAD=∠ABD=72°,则∠OAC=90°72°=18°;
若∠BAD=∠BDA=180°72°2=54°,则∠OAC=90°54°=36°;
若∠ADB=∠ABD=72°,则∠BAD=36°,故∠OAC=90°36°=54°;
②当AC在AB右侧时:
∵∠ABE=108°,且三角形的内角和为180°,
∴只有∠BAD=∠BDA=180°108°2=36°,则∠OAC=90°+36°=126°.
综上所述,当x=18、36、54、126时,△ADB中有两个相等的角。


科目:初中数学 来源: 题型:
【题目】已知三角形的两边及其夹角,求作这个三角形时,第一步骤应为( )
A. 作一条线段等于已知线段
B. 作一个角等于已知角
C. 作两条线段等于已知三角形的边,并使其夹角等于已知角
D. 先作一条线段等于已知线段或先作一个角等于已知角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数![]() 的图像和性质进行了探究,探究过程如下,请补充完整.
的图像和性质进行了探究,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
| … |
|
|
|
| 0 | 1 | 2 | 3 | 4 | … |
| … | 3 |
|
|
| 0 |
| 0 |
| 3 | … |
其中,![]() =____________.
=____________.
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图像的一部分,请画出该图像的另一部分.
(3)观察函数图像,写出两条函数的性质:
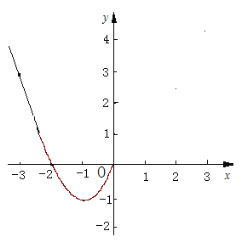
(4)进一步探究函数图像发现:
①函数图像与![]() 轴有__________个交点,所以对应方程
轴有__________个交点,所以对应方程![]() 有___________个实数根;
有___________个实数根;
②方程![]() 有___________个实数根;
有___________个实数根;
③关于![]() 的方程
的方程![]() 有4个实数根,
有4个实数根,![]() 的取值范围是_______________________
的取值范围是_______________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 两点之间,直线最短;
B. 过一点有一条直线平行于已知直线;
C. 有两组边与一组角对应相等的两个三角形全等;
D. 在平面内过一点有且只有一条直线垂直于已知直线
查看答案和解析>>
科目:初中数学 来源: 题型:
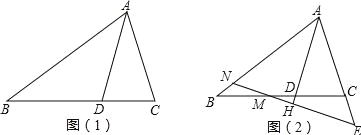
【题目】如图,在△ABC中,BA=BC,D在边CB上,且DB=DA=AC.
(1)如图1,填空∠B= °,∠C= °;
(2)若M为线段BC上的点,过M作直线MH⊥AD于H,分别交直线AB、AC与点N、E,如图2
①求证:△ANE是等腰三角形;
②试写出线段BN、CE、CD之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学测验中,七年级(4)班的平均分为86分,如果把高于平均分的部分记作正数,不足平均分的部分记作负数
(1)李洋得了90分,应记作多少?
(2)刘红的成绩记作-5分,她实际得分是多少?
(3)李洋和刘红相差多少分?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com