
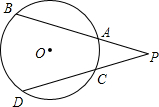
 如图,$\widehat{BD}$=100°,$\widehat{AC}$=30°,则∠P=35°.
如图,$\widehat{BD}$=100°,$\widehat{AC}$=30°,则∠P=35°. 分析 先连接AD、BC,OA、OB、OC、OD,根据圆心角的度数与所对的弧的度数的关系、圆周角定理求出∠BAD和∠ADP的度数,再根据三角形的外角的性质求出∠P的度数.
解答 解:连接AD、BC,OA、OB、OC、OD,
∵$\widehat{BD}$=100°,∴∠BOD=100°,∴∠BAD=50°,
∵$\widehat{AC}$=30°,∴∠AOP=30°,∴∠BAD=50°,
∵∠BAD=∠ADP+∠P,
∴∠P=35°.
点评 本题考查了圆心角与所对的弧的关系、圆周角定理、三角形的外角的性质,根据圆周角定理求出∠BAD和∠ADP的度数是解题的关键,注意要根据题意正确作出辅助线.


科目:初中数学 来源: 题型:填空题
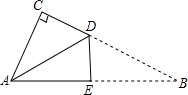 小明拿一张如图的直角三角形纸片ABC,其中∠C=90°,他将纸片沿DE折叠,使点B与点A重合,∠CAD:∠BAD=4:3,则∠CDA的度数为54°.
小明拿一张如图的直角三角形纸片ABC,其中∠C=90°,他将纸片沿DE折叠,使点B与点A重合,∠CAD:∠BAD=4:3,则∠CDA的度数为54°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
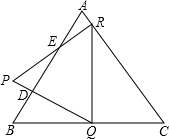 如图,D是边长为4cm的等边△ABC的边AB上的一点,DQ⊥AB交边BC于点Q,RQ⊥BC交边AC于点R,RP⊥AC交边AB于点E,交QD的延长线于点P,若BD=1.1cm,则AE=0.8cm.
如图,D是边长为4cm的等边△ABC的边AB上的一点,DQ⊥AB交边BC于点Q,RQ⊥BC交边AC于点R,RP⊥AC交边AB于点E,交QD的延长线于点P,若BD=1.1cm,则AE=0.8cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
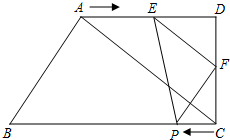 如图,在直角梯形ABCD中,∠D=∠BCD=90°,∠B=60°,AB=$4\sqrt{3}$cm,AD=8cm,直线EF从点A出发沿AD方向匀速运动,速度是2cm/s,运动过程中始终保持EF∥AC,EF交AD于E,交DC于点F;同时,点P从点C出发沿CB方向匀速运动,速度是1cm/s,连接PE、PF,设运动时间为t(s)(0<t<4).
如图,在直角梯形ABCD中,∠D=∠BCD=90°,∠B=60°,AB=$4\sqrt{3}$cm,AD=8cm,直线EF从点A出发沿AD方向匀速运动,速度是2cm/s,运动过程中始终保持EF∥AC,EF交AD于E,交DC于点F;同时,点P从点C出发沿CB方向匀速运动,速度是1cm/s,连接PE、PF,设运动时间为t(s)(0<t<4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.65×10-3 | B. | 65×10-5 | C. | 6.5×10-5 | D. | 6.5×10-4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com