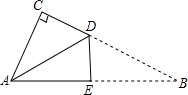
小明拿一张如图的直角三角形纸片ABC.其中∠C=90°.他将纸片沿DE折叠.使点B与点A重合.∠CAD:∠BAD=4:3.则∠CDA的度数为54°．题目和参考答案——青夏教育精英家教网—

14．

小明拿一张如图的直角三角形纸片ABC，其中∠C=90°，他将纸片沿DE折叠，使点B与点A重合，∠CAD：∠BAD=4：3，则∠CDA的度数为54°．

分析设∠CAD=4x，∠BAD=3x，根据翻折的性质可得∠B=∠BAD，然后根据直角三角形两锐角互余列方程求出x，从而得到∠CAD，再根据直角三角形两锐角互余列式计算即可得解．

解答解：∵∠CAD：∠BAD=4：3，
∴∠CAD=4x，∠BAD=3x，
由翻折的性质得，∠B=∠BAD=3x，
在Rt△ABC中，∠BAC+∠B=90°，
∴4x+3x+3x=90°，
解得x=9°，
∴∠CAD=4×9°=36°，
∴∠CDA=90°-∠CAD=90°-36°=54°．
故答案为：54°．

点评本题考查了直角三角形两锐角互余的性质，翻折变换的性质，熟记各性质并列出方程是解题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

4．

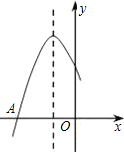如图是二次函数y=ax²+bx+c图象的一部分，图象过点A（-3，0），对称轴为x=-1．给出四个结论：①b²＞4ac；②2a+b=0；③a-b+c=0；④5a＜b．其中正确结论是①④．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

5．菱形一条边长为5，一个内角45°，那么它的面积是$\frac{25\sqrt{2}}{2}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

2．已知一个正数的两个平方根分别为2a+5和3a-15，
（1）求这个正数；
（2）请估算30a的算术平方根在哪两个连续整数之间．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

9．已知：有理数a，b，c满足$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$=$\frac{1}{a+b+c}$，求证：a=-b或b=-c或c=-a．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

19．

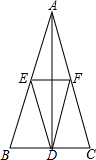文文画了一个等腰△ABC，如图，AB=AC，他又画出BC边上的高AD，在AB上任取一点E过点E作EF∥BC，交AC于点F，然后他写下两个结论．
（1）△AEF是等腰三角形；
（2）△DEF是等腰三角形．
文文的结论正确吗？请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

6．如果一个正整数能表示为两个连续奇数的平方差，那么称这个正整数为“奇特数”，例如：8=3²-1²，16=5²-3²，24=7²-5²；则8、16、24这三个数都是奇特数．
（1）32和2008这两个数是奇特数吗？为什么？
（2）设两个连续奇数是2n-1和2n+1（其中n取正整数），由这两个连续奇数构造的奇特数是8的倍数吗？为什么？
（3）两个连续偶数的平方差（取正数）是奇特数吗？为什么？

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

3．

如图，$\widehat{BD}$=100°，$\widehat{AC}$=30°，则∠P=35°．