
分析 已知等式移项变形后,两边通分并利用同分母分式的加减法则变形,整理后利用三数相乘积为0,三数中至少有一个为0即可得证.
解答 证明:由已知,得$\frac{1}{a}$+$\frac{1}{b}$=$\frac{1}{a+b+c}$-$\frac{1}{c}$,
通分,得$\frac{a+b}{ab}$=$\frac{c-a-b-c}{c(a+b+c)}$,
去分母、移项,得c(a+b)(a+b+c)+ab(a+b)=0,
整理得:(a+b)(ac+bc+c2+ab)=0,
即(a+b)(b+c)(a+c)=0,
可得a+b=0或b+c=0或a+c=0,
则a=-b或b=-c或c=-a.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
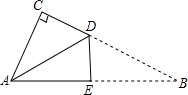 小明拿一张如图的直角三角形纸片ABC,其中∠C=90°,他将纸片沿DE折叠,使点B与点A重合,∠CAD:∠BAD=4:3,则∠CDA的度数为54°.
小明拿一张如图的直角三角形纸片ABC,其中∠C=90°,他将纸片沿DE折叠,使点B与点A重合,∠CAD:∠BAD=4:3,则∠CDA的度数为54°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com