
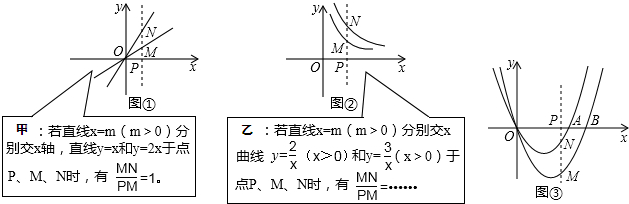
分析 (1)把当x=m分别代入反比例函数的解析式,求出M点的纵坐标和N点的纵坐标,进而求出MN的长,即可求出结果;
(2)当x=m时,则M点的纵坐标为m,N点的纵坐标为2m,进而求出MN的长,d1可求,同理可求出d2;
(3)①由函数的解析式分别求出PM,PN,MN的长,根据等边三角形的性质:三边相等即可求出m的值;
②分两种情况:a:当0<m<3时,过Q作x轴的平行线交直线PK于E;先求出直线PK的解析式,再求出E的坐标,用梯形APEQ的面积减去△EQK的面积即为所求的面积S;b:当m>3时,过Q作x轴的平行线交直线AK于E,先求出直线AK的解析式,再求出E的坐标,用梯形APQE的面积减去△EQK的面积即为所求的面积S.
解答 解:(1)当x=m时,则M点的纵坐标为$\frac{2}{m}$,N点的纵坐标为$\frac{3}{m}$,
∴MN=$\frac{3}{m}$-$\frac{2}{m}$=$\frac{1}{m}$,
∴$\frac{MN}{PM}$=$\frac{\frac{1}{m}}{\frac{2}{m}}$=$\frac{1}{2}$;
(2)当x=m时,则M点的纵坐标为m,N点的纵坐标为2m,
∴MN=2m-m=m,
∴d1=m,
当x=m时,则M点的纵坐标为$\frac{2}{m}$,N点的纵坐标为$\frac{3}{m}$,
∴MN=$\frac{3}{m}$-$\frac{2}{m}$=$\frac{1}{m}$,
∴d2=$\frac{1}{m}$;
(3)①OP=m,PM=|4m-m2|=m|4-m|,PN=|3m-m2|=m|3-m|,MN=m,
由题意,得m|4-m|=m或m|3-m|=m,
解得m=5或m=3或m=4或m=2,
当m=3时,点P与点A重合,当m=4时,点P与点B重合,
∴m=2或5;
②分两种情况:a:当0<m<3时,如图1所示: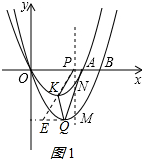 过Q作x轴的平行线交直线PK于E;
过Q作x轴的平行线交直线PK于E;
设直线PK的解析式为y=kx+b,
∵抛物线y=x2-4x=(x-2)2-4,
∴Q(2,-4),
∵y=x2-3x=(x-$\frac{3}{2}$)2-$\frac{9}{4}$,
∴K($\frac{3}{2}$,-$\frac{9}{4}$),
把点K($\frac{3}{2}$,-$\frac{9}{4}$),P(m,0)代入得:$\left\{\begin{array}{l}{-\frac{3}{2}k+b=-\frac{9}{4}}\\{km+b=0}\end{array}\right.$,
解得:k=$\frac{9}{4m-6}$,b=-$\frac{9m}{4m-6}$,
∴y=$\frac{9}{4m-6}$x-$\frac{9m}{4m-6}$,
当y=-4时,$\frac{9}{4m-6}$x-$\frac{9m}{4m-6}$=-4,
解得:x=$\frac{24-7m}{9}$,
∴E($\frac{24-7m}{9}$,-4),
∴EQ=2-$\frac{24-7m}{9}$=$\frac{7m-6}{9}$,
∴S梯形APEQ=$\frac{1}{2}$(3-m+$\frac{7m-6}{9}$)×4=$\frac{42-9m}{9}$,
S△EQK=$\frac{1}{2}$×$\frac{7m-6}{9}$(4-$\frac{9}{4}$)=$\frac{49m-42}{72}$,
∴以K、Q、A、P四点为顶点的四边形面积S=S梯形APEQ-S△EQK
=$\frac{42-9m}{9}$-$\frac{49m-42}{72}$=$\frac{42-9m}{8}$(m≠$\frac{6}{7}$);
b:当m>3时,过Q作x轴的平行线交直线AK于E,如图2所示: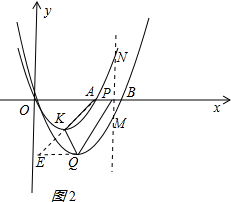
∵抛物线y=x2-3x,当y=0时,x=0或x=3,∴A(3,0),
设直线AK的解析式为y=kx+b
,把点A(3,0),K($\frac{3}{2}$,-$\frac{9}{4}$)代入得:$\left\{\begin{array}{l}{\frac{3}{2}k+b=-\frac{9}{4}}\\{3k+b=0}\end{array}\right.$,
解得:k=$\frac{3}{2}$,b=$-\frac{9}{2}$,
∴y=$\frac{3}{2}$x-$\frac{9}{2}$,当y=-4时,$\frac{3}{2}$x-$\frac{9}{2}$=-4,
解得:x=$\frac{1}{3}$,∴E($\frac{1}{3}$,-4),
∴EQ=2-$\frac{1}{3}$=$\frac{5}{3}$,
∴S△EQK=$\frac{1}{2}$×$\frac{5}{3}$×(4-$\frac{9}{4}$)=$\frac{35}{24}$,
S梯形APQE=$\frac{1}{2}$(m-3+$\frac{5}{3}$)×4=2m-$\frac{8}{3}$,
∴S=S梯形APQE-S△EQK=2m-$\frac{8}{3}$-$\frac{35}{24}$=$\frac{16m-33}{8}$;
综上所述:当0<m<3,且m≠$\frac{6}{7}$时,S=$\frac{42-9m}{8}$;当m>3时,S=$\frac{16m-33}{8}$.
点评 本题考查了一次函数、反比例函数、二次函数的各种性质以及等边三角形的性质和梯形的面积公式、三角形的面积公式等知识;题目的综合性较强,难度很大,对学生的解题能力要求很高,特别是(3)的②中,需要通过作辅助线用函数解析式求出点的坐标才能得出面积.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:选择题
| A. | 3x2+5x2=8x4 | B. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | ||
| C. | $\frac{1}{x+1}$-$\frac{1}{x-1}$=$\frac{2}{{{x^2}-1}}$ | D. | (-$\frac{1}{2}$m2n)2=$\frac{1}{4}$m4n2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
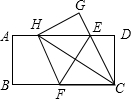 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,则线段BF的取值范围为3≤BF≤4.
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,则线段BF的取值范围为3≤BF≤4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
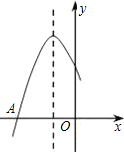 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出四个结论:①b2>4ac;②2a+b=0;③a-b+c=0;④5a<b.其中正确结论是①④.
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出四个结论:①b2>4ac;②2a+b=0;③a-b+c=0;④5a<b.其中正确结论是①④.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
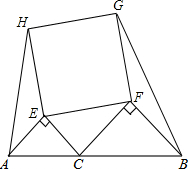 如图,点C在线段AB上,分别以AC和CB为斜边向上作等腰直角△AEC和△CFB,已知这两个等腰直角三角形的直角边分别为6cm和8cm,又以EF为边向上作正方形EFGH,连接AH,BG,则四边形ABGH的面积为222cm2.
如图,点C在线段AB上,分别以AC和CB为斜边向上作等腰直角△AEC和△CFB,已知这两个等腰直角三角形的直角边分别为6cm和8cm,又以EF为边向上作正方形EFGH,连接AH,BG,则四边形ABGH的面积为222cm2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com