
分析 ①通过反例即可判断;
②把m=-3代入,然后化成顶点式即可判断;
③求得与x轴的交点,进而求得|x1-x2|的值,即可判断;
④由y=2mx2+(1-m)x-1-m=(2x2-x-1)m+x-1,可知当2x2-x-1=0时,y的值与m无关,此时x1=1,x2=-$\frac{1}{2}$,当x1=1,y=0;当x2=-$\frac{1}{2}$时,y2=-$\frac{3}{2}$,从而判定函数图象总经过两个定点(1,0),(-$\frac{1}{2}$,-$\frac{3}{2}$).
解答 解:①假命题;
当m=0时,y=x-1为一次函数
与坐标轴只有两个交点,
②真命题;
当m=-3时,y=-6x2+4x+2=-6(x-$\frac{1}{3}$)2+$\frac{8}{3}$,
∴顶点坐标是($\frac{1}{3}$,$\frac{8}{3}$),
③真命题;
当m>0时,由y=0得:△=(1-m)2-4×2m(-1-m)=(3m+1)2,
∴x=$\frac{m-1±(3m+1)}{4m}$,
∴x1=1,x2=-$\frac{1}{2}$-$\frac{1}{2m}$,
∴|x1-x2|=$\frac{3}{2}$+$\frac{1}{2m}$>$\frac{3}{2}$,
∴函数图象截x轴所得的线段长度大于$\frac{3}{2}$;
④真命题;
当m≠0时,y=2mx2+(1-m)x-1-m=(2x2-x-1)m+x-1,
当2x2-x-1=0时,y的值与m无关
此时x1=1,x2=-$\frac{1}{2}$,
当x1=1,y=0;当x2=-$\frac{1}{2}$时,y2=-$\frac{3}{2}$,
∴函数图象总经过两个定点(1,0),(-$\frac{1}{2}$,-$\frac{3}{2}$).
点评 本题考查了二次函数的性质,抛物线与二次函数的交点,熟练掌握二次函数的性质是解题的关键.


科目:初中数学 来源: 题型:选择题
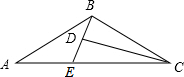 如图,D为△ABC内一点,CD平分∠ACB,BE⊥CD,垂足为D,交AC于点E,∠A=∠ABE,AC=5,BC=3,则BD的长为( )
如图,D为△ABC内一点,CD平分∠ACB,BE⊥CD,垂足为D,交AC于点E,∠A=∠ABE,AC=5,BC=3,则BD的长为( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
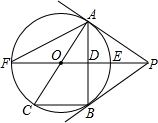 如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
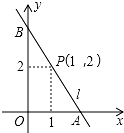 如图,直线l经过点P(1,2),与坐标轴交于A(a,0),B(0,b)两点(其中a<b,如果a+b=6,那么tan∠ABO的值为$\frac{1}{2}$.
如图,直线l经过点P(1,2),与坐标轴交于A(a,0),B(0,b)两点(其中a<b,如果a+b=6,那么tan∠ABO的值为$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
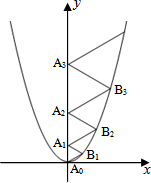 二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,A1,A2,A3,…,A2008在y轴的正半轴上,B1,B2,B3,…,B2008在二次函数y=$\frac{2}{3}$x2第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2007B2008A2008都为等边三角形,请计算△A0B1A1的边长=1;△A1B2A2的边长=2;△A2007B2008A2008的边长=2008.
二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,A1,A2,A3,…,A2008在y轴的正半轴上,B1,B2,B3,…,B2008在二次函数y=$\frac{2}{3}$x2第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2007B2008A2008都为等边三角形,请计算△A0B1A1的边长=1;△A1B2A2的边长=2;△A2007B2008A2008的边长=2008.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
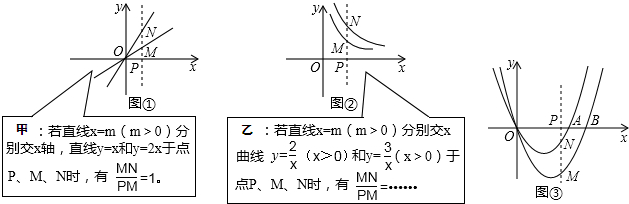
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com