
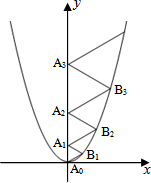
 ���κ���y=$\frac{2}{3}$x2��ͼ����ͼ��ʾ����A0λ������ԭ�㣬A1��A2��A3������A2008��y����������ϣ�B1��B2��B3������B2008�ڶ��κ���y=$\frac{2}{3}$x2��һ����ͼ���ϣ�����A0B1A1����A1B2A2����A2B3A3��������A2007B2008A2008��Ϊ�ȱ������Σ�������A0B1A1�ı߳�=1����A1B2A2�ı߳�=2����A2007B2008A2008�ı߳�=2008��
���κ���y=$\frac{2}{3}$x2��ͼ����ͼ��ʾ����A0λ������ԭ�㣬A1��A2��A3������A2008��y����������ϣ�B1��B2��B3������B2008�ڶ��κ���y=$\frac{2}{3}$x2��һ����ͼ���ϣ�����A0B1A1����A1B2A2����A2B3A3��������A2007B2008A2008��Ϊ�ȱ������Σ�������A0B1A1�ı߳�=1����A1B2A2�ı߳�=2����A2007B2008A2008�ı߳�=2008�� ���� ���ڡ�A0B1A1����A1B2A2����A2B3A3���������ǵȱ������Σ���ˡ�B1A0x=30�㣬���������A0B1A1�ı߳���Ȼ���ʾ��B1�����꣬���������ߵĽ���ʽ�м�����á�A0B1A1�ı߳�����ͬ���ķ�������á�A0B1A1����A1B2A2����A2B3A3�����ı߳���Ȼ����ݸ��߳����ص��ܽ�������һ�㻯���ɣ�Ȼ�������ù����������A2007B2008A2008�ı߳����ɣ�
��� �⣺���A0B1A1�ı߳�Ϊm1����B1��$\frac{\sqrt{3}{m}_{1}}{2}$��$\frac{{m}_{1}}{2}$����
���������ߵĽ���ʽ�еã�$\frac{2}{3}$����$\frac{\sqrt{3}{m}_{1}}{2}$��2=$\frac{{m}_{1}}{2}$��
���m1=0����ȥ����m1=1��
�ʡ�A0B1A1�ı߳�Ϊ1��
ͬ������á�A1B2A2�ı߳�Ϊ2��
��
�������ƣ���AnBn+1An+1�ı߳�Ϊn+1��
�ʡ�A2007B2008A2008�ı߳�Ϊ2008��
�ʴ�Ϊ1��2��2008��
���� ���⿼���˶��κ������ۺ����ã��ؼ��Ǹ����������ε����ʱ�ʾ������꣬���������߽���ʽ���������εı߳����õ����ɣ�


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �Խ����ƽ�ֵ��ı�����ƽ���ı��� | |
| B�� | �Խ����ƽ������ȵ��ı����Ǿ��� | |
| C�� | �Խ����ƽ���Ҵ�ֱ���ı��������� | |
| D�� | �Խ�������Ҵ�ֱ���ı����������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
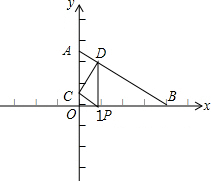 ��ֱ֪��������ֽƬOAB�����С�AOB=90�㣬OA=3��OB=4����P��t��0����OB���ϵĶ��㣬����P��PC��AB��y���ڵ�C��ͬʱ����P��PD��x�ύAB�ڵ�D
��ֱ֪��������ֽƬOAB�����С�AOB=90�㣬OA=3��OB=4����P��t��0����OB���ϵĶ��㣬����P��PC��AB��y���ڵ�C��ͬʱ����P��PD��x�ύAB�ڵ�D�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
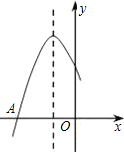 ��ͼ�Ƕ��κ���y=ax2+bx+cͼ���һ���֣�ͼ�����A��-3��0�����Գ���Ϊx=-1�������ĸ����ۣ���b2��4ac����2a+b=0����a-b+c=0����5a��b��������ȷ�����Ǣ٢ܣ�
��ͼ�Ƕ��κ���y=ax2+bx+cͼ���һ���֣�ͼ�����A��-3��0�����Գ���Ϊx=-1�������ĸ����ۣ���b2��4ac����2a+b=0����a-b+c=0����5a��b��������ȷ�����Ǣ٢ܣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com