
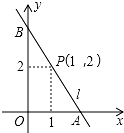
 如图,直线l经过点P(1,2),与坐标轴交于A(a,0),B(0,b)两点(其中a<b,如果a+b=6,那么tan∠ABO的值为$\frac{1}{2}$.
如图,直线l经过点P(1,2),与坐标轴交于A(a,0),B(0,b)两点(其中a<b,如果a+b=6,那么tan∠ABO的值为$\frac{1}{2}$. 分析 根据题意得出b=2-k,a=4+k,进而代入函数关系式求出k的值进而求出a,b的值即可得出答案.
解答 解:设直线AB的解析式为:y=kx+b,
∵直线l经过点P(1,2),
∴k+b=2,
∴b=2-k,
∵a+b=6,k+b=2,
∴a=4+k,
∵直线l经过点P(1,2),与坐标轴交于A(a,0),
∴ak+b=0,
∴(4+k)k+2-k=0,
解得:k1=-1,k2=-2,
当k=-1,则a=3,b=3,不合题意舍去;
∴k=-2,则a=2,b=4,
∴tan∠ABO的值为:$\frac{2}{4}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 此题主要考查了一次函数图象上点的坐标特征以及锐角三角函数的定义等知识,根据题意得出关于k的一元二次方程是解题关键.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:填空题
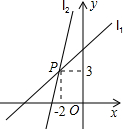 如图,一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2相交于点P,则关于x的不等式k1x+b1>k2x+b2的解集是x<-2.
如图,一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2相交于点P,则关于x的不等式k1x+b1>k2x+b2的解集是x<-2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是一座人行天桥的引桥部分的示意图,上桥通道由两段互相平行并且与地面成36°角的楼梯AD、BE和一段水平平台DE构成.已知天桥高度BC≈4.5米,引桥水平跨度AC=7米.
如图是一座人行天桥的引桥部分的示意图,上桥通道由两段互相平行并且与地面成36°角的楼梯AD、BE和一段水平平台DE构成.已知天桥高度BC≈4.5米,引桥水平跨度AC=7米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,则线段BF的取值范围为3≤BF≤4.
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,则线段BF的取值范围为3≤BF≤4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
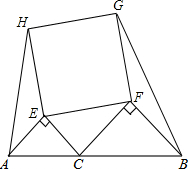 如图,点C在线段AB上,分别以AC和CB为斜边向上作等腰直角△AEC和△CFB,已知这两个等腰直角三角形的直角边分别为6cm和8cm,又以EF为边向上作正方形EFGH,连接AH,BG,则四边形ABGH的面积为222cm2.
如图,点C在线段AB上,分别以AC和CB为斜边向上作等腰直角△AEC和△CFB,已知这两个等腰直角三角形的直角边分别为6cm和8cm,又以EF为边向上作正方形EFGH,连接AH,BG,则四边形ABGH的面积为222cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在雷达探测区内,可以建立平面直角坐标系表示位置,当我方两架飞机在A(-1,2)与B(3,2)位置,可疑飞机在(-1,3)位置,你能找到这个直角坐标系的横,纵坐标轴的位置吗?把它们表示出来,并确定可疑飞机的所处方位.
如图,在雷达探测区内,可以建立平面直角坐标系表示位置,当我方两架飞机在A(-1,2)与B(3,2)位置,可疑飞机在(-1,3)位置,你能找到这个直角坐标系的横,纵坐标轴的位置吗?把它们表示出来,并确定可疑飞机的所处方位.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com