
分析 从∠APB为直角、∠ABP为直角、∠PAB为直角三个方面进行解答.当因为O为AB的中点,所以OP=$\frac{1}{2}$AB时,∠APB为直角;过点B作AB的垂线,分别交x轴和y=2于点D、P,过点B作x轴的垂线,分别交x轴和y=2于点C、E,分别求出BC、BE、CD的长,根据△BCD∽△BEP,求出EP的长,得到∠ABP为直角时点P的坐标,同理,求出∠PAB为直角时点P的坐标.
解答 解:根据反比例函数的性质,O为AB的中点,当OP=$\frac{1}{2}$AB时,∠APB为直角,
∵A点的坐标(3,4),∴B点的坐标(-3,-4),∴AB=2OA=2OB=10,
设P点的坐标为(x,2),
则x2+22=52,x=±$\sqrt{21}$,
∴点P的坐标为($\sqrt{21}$,2),(-$\sqrt{21}$,2);
如图:过点B作AB的垂线,分别交x轴和y=2于点D、P,过点B作x轴的垂线,分别交x轴和y=2于点C、E,
由题意可知:BC=4,BE=6,
由射影定理得:OD=$\frac{25}{3}$,CD=$\frac{16}{3}$,
∵△BCD∽△BEP,
∴$\frac{CD}{PE}$=$\frac{BC}{BE}$
PE=$\frac{\frac{16}{3}×6}{4}$=8,
∴点P的坐标为(-11,2);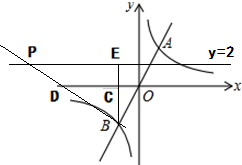
如图:同理可以求得:DP=$\frac{8}{3}$,
∴点P的坐标为($\frac{17}{3}$,2)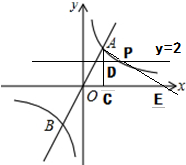
∴点P的坐标为:($\sqrt{21}$,2);(-$\sqrt{21}$,2);(-11,2);($\frac{17}{3}$,2).
点评 本题考查了反比例函数、直角三角形和相似三角形的性质,体现了数形结合的思想,解题的关键是找出所有构成直角三角形的情形,然后根据图形的特点逐一进行解答,解答时,辅助线的正确添加非常重要.


科目:初中数学 来源: 题型:选择题
| A. | 1.00553×109 | B. | 1.00553×1010 | C. | 1.00553×1011 | D. | 1.00553×1012 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
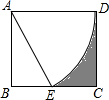 如图,矩形纸片ABCD,AD=4,以A为圆心画弧交于BC中点E,则图中围成阴影部分图形的周长为9.4.(其中π取3,$\sqrt{3}$≈1.7)
如图,矩形纸片ABCD,AD=4,以A为圆心画弧交于BC中点E,则图中围成阴影部分图形的周长为9.4.(其中π取3,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
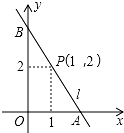 如图,直线l经过点P(1,2),与坐标轴交于A(a,0),B(0,b)两点(其中a<b,如果a+b=6,那么tan∠ABO的值为$\frac{1}{2}$.
如图,直线l经过点P(1,2),与坐标轴交于A(a,0),B(0,b)两点(其中a<b,如果a+b=6,那么tan∠ABO的值为$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 垂直于弦的直径平分弦 | |
| B. | 若a>b,c>0,则ac>bc | |
| C. | 反比例函数y=$\frac{k}{x}$,当k>0时,y随x的增大而减少 | |
| D. | 对角线互相平分且垂直的四边形是菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
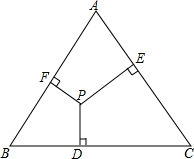 有一块等边三角形的空地,小明和小亮想在这块空地上找到一点,使得这一点到三边的距离之和最短,他们做了几次实验,发现无论三角形内的哪一点到三边的距离之和都是相等的.于是他们编了一道几何题:如图,已知点P为正△ABC内一点,点P到BC,CA,AB的距离分别为PD,PE,PF,试说明PD+PE+PF总是一个定值.这个定值与什么有关?你发现这个事实了吗?你能解出他们编的数学问题吗?
有一块等边三角形的空地,小明和小亮想在这块空地上找到一点,使得这一点到三边的距离之和最短,他们做了几次实验,发现无论三角形内的哪一点到三边的距离之和都是相等的.于是他们编了一道几何题:如图,已知点P为正△ABC内一点,点P到BC,CA,AB的距离分别为PD,PE,PF,试说明PD+PE+PF总是一个定值.这个定值与什么有关?你发现这个事实了吗?你能解出他们编的数学问题吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com