
【题目】如图,在△ABC中,DE垂直平分AB,分别交![]() 的边
的边![]() 、
、![]() 于
于![]() 、
、![]() ,
,![]() 平分
平分![]() .设
.设![]() ,
,![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 为等腰三角形时,求∠C的度数.
为等腰三角形时,求∠C的度数.

【答案】(1)![]() ;(2)∠C=45°或72°.
;(2)∠C=45°或72°.
【解析】
(1)根据线段垂直平分线的性质和角平分线定义求出∠BAC的度数,然后利用三角形内角和定理列式整理可得答案;
(2)分情况讨论:①若∠B=∠BAC,②若∠B=∠C,③若∠C=∠BAC,分别列式计算即可.
解:(1)∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B=![]() ,
,
∵AE平分∠BAC,
∴∠BAC=2∠BAE=![]() ,
,
∵∠B+∠BAC+∠C=180°,
∴![]() ,
,
![]() ;
;
(2)△ABC为等腰三角形时,∠B=∠BAC或∠B=∠C或∠C=∠BAC,
①若∠B=∠BAC,则y=2y,
不符合题意;
②若∠B=∠C,则x=y,
∴![]() ,
,
解得:![]() ;
;
∴![]() ;
;
③若∠C=∠BAC,则![]() ,
,
解得:![]() ,
,
∴![]() ,
,
∴当△ABC为等腰三角形时,∠C=45°或72°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥CD,∠B=70°,∠BCE=20°,∠CEF=130°,请判断AB与EF的位置关系,并说明理由.
解: ,理由如下:
∵AB∥CD,
∴∠B=∠BCD,( )
∵∠B=70°,
∴∠BCD=70°,( )
∵∠BCE=20°,
∴∠ECD=50°,
∵∠CEF=130°,
∴ + =180°,
∴EF∥ ,( )
∴AB∥EF.( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以O为原点的直角坐标系中,A点的坐标为(0,3),直线x=-3交x轴于点B,P为线段AB上一动点,作直线PC⊥PO,交于直线x=﹣3于点C。过P点作直线MN平行于x轴,交y轴于M,交直线x=﹣3于点N。
(1)当点C在第二象限时,求证:△OPM≌△PCN;
(2)设AP长为m,以P、O、B、C为顶点的四边形的面积为S,请求出S与M之间的函数关系式,并写出自变量m的取值范围;
(3)当点P在线段AB上移动时,点C也随之在直线x=-3上移动,△PBC是否可能成为等腰三角形?如果可能,求出所有能使△PBC成为等腰三角形的点P的坐标,如果不可能,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把平面内一条数轴![]() 绕原点
绕原点![]() 逆时针旋转角
逆时针旋转角![]() 得到另一条数轴
得到另一条数轴![]() 轴和
轴和![]() 轴构成一个平面斜坐标系.过点
轴构成一个平面斜坐标系.过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 轴于点
轴于点![]() .若点
.若点![]() 在
在![]() 轴上对应的实数为
轴上对应的实数为![]() ,点
,点![]() 在
在![]() 轴上对应的实数为
轴上对应的实数为![]() ,则成有序实数对
,则成有序实数对![]() 为点
为点![]() 的斜坐标.
的斜坐标.
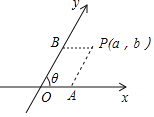
(1)在某平面斜坐标系中,已知![]() ,点
,点![]() 的斜坐标为
的斜坐标为![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,求点
轴对称,求点![]() 的斜坐标.
的斜坐标.
(2)某平面斜坐标系中,已知点![]() ,求出点
,求出点![]() 关于
关于![]() 轴、
轴、![]() 轴的对称点
轴的对称点![]() 点、
点、![]() 点的斜坐标.(用含
点的斜坐标.(用含![]() 及
及![]() 的式子表示).
的式子表示).
(3)直接写出点![]() 关于原点对称的点的斜坐标是_________.
关于原点对称的点的斜坐标是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公元前5世纪,毕达哥拉斯学派中的一名成员希伯索斯发现了无理数![]() ,导致了第一次数学危机.
,导致了第一次数学危机.![]() 是无理数的证明如下:
是无理数的证明如下:
假设![]() 是有理数,那么它可以表示成
是有理数,那么它可以表示成![]() (
(![]() 与
与![]() 是互质的两个正整数).于是
是互质的两个正整数).于是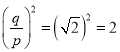 ,所以,
,所以,![]() .于是
.于是![]() 是偶数,进而
是偶数,进而![]() 是偶数.从而可设
是偶数.从而可设![]() ,所以
,所以![]() ,
,![]() ,于是可得
,于是可得![]() 也是偶数.这与“
也是偶数.这与“![]() 与
与![]() 是互质的两个正整数”矛盾,从而可知“
是互质的两个正整数”矛盾,从而可知“![]() 是有理数”的假设不成立,所以,
是有理数”的假设不成立,所以,![]() 是无理数.这种证明“
是无理数.这种证明“![]() 是无理数”的方法是( )
是无理数”的方法是( )
A.综合法B.反证法C.举反例法D.数学归纳法
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆心都在x轴正半轴上的半圆O1 , 半圆O2 , …,半圆On与直线l相切.设半圆O1 , 半圆O2 , …,半圆On的半径分别是r1 , r2 , …,rn , 则当直线l与x轴所成锐角为30°,且r1=1时,r2018=.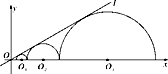
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC于点F.
(1)判断DF与是⊙O的位置关系,并证明你的结论。
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD内有两条相交线段MN,EF,M,N,E,F分别在边AB,CD,AD,BC上.小明认为:若MN=EF,则MN⊥EF;小亮认为:若MN⊥EF,则MN=EF.你认为( )

A. 仅小明对 B. 仅小亮对 C. 两人都对 D. 两人都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A(2,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(a,b),且a=![]() +
+![]() -6
-6
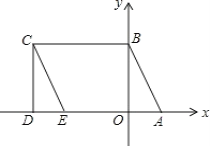
(1)求点C的坐标;
(2)求点E的坐标;
(3)点P是CE上一动点,设∠CBP=x°,∠PAD=y°,∠BPA=z°,确定x,y,z之间的数量c关系,并证明你的结论
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com