练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】公元前5世纪，毕达哥拉斯学派中的一名成员希伯索斯发现了无理数，导致了第一次数学危机.是无理数的证明如下：

    假设是有理数，那么它可以表示成（与是互质的两个正整数）.于是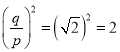，所以，.于是是偶数，进而是偶数.从而可设，所以，，于是可得也是偶数.这与“与是互质的两个正整数”矛盾，从而可知“是有理数”的假设不成立，所以，是无理数.这种证明“是无理数”的方法是( )

    A.综合法B.反证法C.举反例法D.数学归纳法

    【答案】B

    【解析】

    利用反证法的一般步骤是：①假设命题的结论不成立；②从这个假设出发，经过推理论证，得出矛盾；③由矛盾判定假设不正确，从而肯定原命题的结论正确，进而判断即可．

    解：由题意可得：这种证明“是无理数”的方法是反证法．
    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在等边三角形中，在边上取两点、，使．若，，， 则以，，为边长的三角形的形状为（ ）

    A.锐角三角形B.直角三角形C.钝角三角形D.随，，的值而定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，等腰Rt△CEF的斜边CE在正方形ABCD的边BC的延长线上，CF>BC，取线段AE的中点M 。

    （1）求证：MD=MF,MD⊥MF
    （2）若Rt△CEF绕点C顺时针旋转任意角度（如图2），其他条件不变。（1）中的结论是否仍然成立，若成立，请证明，若不成立，请说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】直线的解析式为，分别交轴、轴于点．

    （1）写出两点的坐标，并画出直线的图象．（不需列表）；

    （2）将直线向左平移4个单位得到交轴于点．作出的图象，的解析式是___________．

    （3）过的顶点能否画出直线把分成面积相等的两部分？若能，可以画出几条？直接写出满足条件的直线解析式．（不必在图中画出直线）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是某小区的一个健身器材，已知BC=0.15m，AB=2.70m，∠BOD=70°，求端点A到地面CD的距离（精确到0.1m）．（参考数据：sin70°≈0.94，cos70°≈0.34，tan70°≈2.75）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，DE垂直平分AB，分别交的边、于、，平分．设，．

    （1）求关于的函数关系式；

    （2）当为等腰三角形时，求∠C的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，顶点A，C分别在坐标轴上，顶点B的坐标为（4，2）．过点D（0，3）和E（6，0）的直线分别与AB，BC交于点M，N．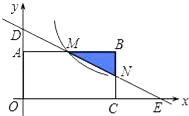

    （1）求直线DE的解析式和点M的坐标；
    （2）若反比例函数 （x＞0）的图象经过点M，求该反比例函数的解析式，并通过计算判断点N是否在该函数的图象上；
    （3）若反比例函数 （x＞0）的图象与△MNB有公共点，请直接写出m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中AB=AC=4，∠C=72°，D是AB中点，点E在AC上，DE⊥AB，则cosA的值为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    同步练习册答案