
【题目】如图,在等边三角形![]() 中,在
中,在![]() 边上取两点
边上取两点![]() 、
、![]() ,使
,使![]() .若
.若![]() ,
,![]() ,
,![]() , 则以
, 则以![]() ,
,![]() ,
,![]() 为边长的三角形的形状为( )
为边长的三角形的形状为( )

A.锐角三角形B.直角三角形C.钝角三角形D.随![]() ,
,![]() ,
,![]() 的值而定
的值而定
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②当x>﹣1时,y随x增大而减小;③a+b+c<0;④若方程ax2+bx+c﹣m=0没有实数根,则m>2; ⑤3a+c<0.其中正确结论的个数是( )
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,∠AOC的平分线交AB于点D,E为BC的中点,已知A(0,4)、C(5,0),二次函数 ![]() 的图象抛物线经过A、C两点.
的图象抛物线经过A、C两点.

(1)求该二次函数的表达式;
(2)F,G分别为x轴、y轴上的动点,首尾顺次连接D、E、F、G构成四边形DEFG,求四边形DEFG周长的最小值;
(3)抛物线上是否存在点P,使△ODP的面积为8?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形BEDG和矩形BNDQ中,BE=BN,DE=DN.
(1)将两个矩形叠合成如图10,求证:四边形ABCD是菱形;
(2)若菱形ABCD的周长为20,BE=3,求矩形BEDG的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥CD,∠B=70°,∠BCE=20°,∠CEF=130°,请判断AB与EF的位置关系,并说明理由.
解: ,理由如下:
∵AB∥CD,
∴∠B=∠BCD,( )
∵∠B=70°,
∴∠BCD=70°,( )
∵∠BCE=20°,
∴∠ECD=50°,
∵∠CEF=130°,
∴ + =180°,
∴EF∥ ,( )
∴AB∥EF.( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,点E、F、G、H分别在AB、BC、CD、AD边上且AE=CG,AH=CF.
(1)求证:四边形EFGH是平行四边形;
(2)如果AB=AD,且AH=AE,求证:四边形EFGH是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线a 、b被直线c所截,现给出下列四种条件:
①∠2=∠6 ②∠2=∠8 ③∠1+∠4=180° ④∠3=∠8,其中能判断是a∥b的条件的序号是( )

A. ①② B. ①③ C. ①④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公元前5世纪,毕达哥拉斯学派中的一名成员希伯索斯发现了无理数![]() ,导致了第一次数学危机.
,导致了第一次数学危机.![]() 是无理数的证明如下:
是无理数的证明如下:
假设![]() 是有理数,那么它可以表示成
是有理数,那么它可以表示成![]() (
(![]() 与
与![]() 是互质的两个正整数).于是
是互质的两个正整数).于是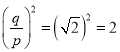 ,所以,
,所以,![]() .于是
.于是![]() 是偶数,进而
是偶数,进而![]() 是偶数.从而可设
是偶数.从而可设![]() ,所以
,所以![]() ,
,![]() ,于是可得
,于是可得![]() 也是偶数.这与“
也是偶数.这与“![]() 与
与![]() 是互质的两个正整数”矛盾,从而可知“
是互质的两个正整数”矛盾,从而可知“![]() 是有理数”的假设不成立,所以,
是有理数”的假设不成立,所以,![]() 是无理数.这种证明“
是无理数.这种证明“![]() 是无理数”的方法是( )
是无理数”的方法是( )
A.综合法B.反证法C.举反例法D.数学归纳法
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com