
【题目】已知矩形BEDG和矩形BNDQ中,BE=BN,DE=DN.
(1)将两个矩形叠合成如图10,求证:四边形ABCD是菱形;
(2)若菱形ABCD的周长为20,BE=3,求矩形BEDG的面积.

【答案】(1)证明见解析;(2)27.
【解析】
(1)作AR⊥BC于R,AS⊥CD于S,根据题意先证出四边形ABCD是平行四边形,再由BC=CD得平行四边形ABCD是菱形;
(2)根据菱形的性质得出AD的长,进而得出AE的长,再利用矩形面积公式求出即可.
解:(1)答:四边形ABCD是菱形.
证明:作AR⊥BC于R,AS⊥CD于S,
由题意知:AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,
∵矩形BEDG和矩形BNDQ中,BE=BN,DE=DN,
∴两个矩形全等,
∴AR=AS,
∵ARBC=ASCD,
∴BC=CD,
∴平行四边形ABCD是菱形;
(2)解:∵菱形ABCD的周长为20,
∴AD=AB=BC=CD=5,
∵BE=3,
∴AE=4,
∴DE=5+4=9,
∴矩形BEDG的面积为:3×9=27.



科目:初中数学 来源: 题型:
【题目】如图所示,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字0所对应的点与数轴上的数﹣2所对应的点重合,再让圆沿着数轴按顺时针方向滚动,那么数轴上的数﹣2016将与圆周上的哪个数字重合( ) 
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全,小明骑单车上学,当他骑了一段时,想起要买文具,于是又折回到刚经过的文具店,买到文具后继续去学校,下图是他本次所用的时间与离家路程的关系示意图,根据图中提供的信息回答下列问题:

(1)小明家到学校的路程是___________米;小明在文具店停留了__________分钟.
(2)本次上学途中,小明一共行驶了多少米?
(3)我们认为骑单车的速度超过300米/分钟就超越了安全限度,问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形 ABCD 中,放入六个形状大小相同的长方形,所标尺寸如图所示, 则图中阴影部分面积为( )

A. 44cm2B. 36cm2C. 96 cm2D. 84cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像相交于点
的图像相交于点![]() ,一次函数
,一次函数![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
(1)求![]() 和
和![]() 的值;
的值;
(2)点![]() 在
在![]() 轴正半轴上,且
轴正半轴上,且![]() 的面积为1,求点
的面积为1,求点![]() 坐标;
坐标;
(3)在(2)的条件下,点![]() 是一次函数
是一次函数![]() 上一点,点
上一点,点![]() 是反比例函数
是反比例函数![]() 图像上一点,且点
图像上一点,且点![]() 、
、![]() 都在
都在![]() 轴上方.如果以
轴上方.如果以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形,请直接写出点
为顶点的四边形为平行四边形,请直接写出点![]() 、
、![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形![]() 中,在
中,在![]() 边上取两点
边上取两点![]() 、
、![]() ,使
,使![]() .若
.若![]() ,
,![]() ,
,![]() , 则以
, 则以![]() ,
,![]() ,
,![]() 为边长的三角形的形状为( )
为边长的三角形的形状为( )

A.锐角三角形B.直角三角形C.钝角三角形D.随![]() ,
,![]() ,
,![]() 的值而定
的值而定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为点E.连接DE, 则线段DE与线段AC有怎样的数量关系?请证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,三角形ABC的顶点坐标分别为![]() ,
,![]() ,
,![]() ,把三角形ABC进行平移,平移后得到三角形
,把三角形ABC进行平移,平移后得到三角形![]() ,且三角形ABC内任意点
,且三角形ABC内任意点![]() 平移后的对应点为
平移后的对应点为![]() .
.
(1)面出平移后的图形;
(2)三角形ABC是经过怎样平移后得到三角形![]() 的?写出三个顶点
的?写出三个顶点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(3)求三角形ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某小区的一个健身器材,已知BC=0.15m,AB=2.70m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1m).(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)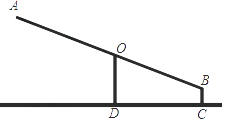
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com