
【题目】如图,在长方形 ABCD 中,放入六个形状大小相同的长方形,所标尺寸如图所示, 则图中阴影部分面积为( )

A. 44cm2B. 36cm2C. 96 cm2D. 84cm2
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2, 0)、(2,1)、(1,1)、(1,2)、(2,2)…根据这个规律,第2019个点的坐标为( )

A. (45,6)B. (45,13)C. (45,22)D. (45,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种小商品的成本价为10元/kg,市场调查发现,该产品每天的销售量w(kg)与销售价x(元/kg)有如下关系w=﹣2x+100,设这种产品每天的销售利润为y(元).
(1)求y与x之间的函数关系式;
(2)当售价定为多少元时,每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践操作:如图,在 ![]() 中,∠ABC=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法):
中,∠ABC=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法):
(1)作∠BCA的角平分线,交AB于点O;
(2)以O为圆心,OB为半径作圆.
综合运用:在你所作的图中,
(3)AC与⊙O的位置关系是(直接写出答案);
(4)若BC=6,AB=8,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,∠AOC的平分线交AB于点D,E为BC的中点,已知A(0,4)、C(5,0),二次函数 ![]() 的图象抛物线经过A、C两点.
的图象抛物线经过A、C两点.

(1)求该二次函数的表达式;
(2)F,G分别为x轴、y轴上的动点,首尾顺次连接D、E、F、G构成四边形DEFG,求四边形DEFG周长的最小值;
(3)抛物线上是否存在点P,使△ODP的面积为8?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形BEDG和矩形BNDQ中,BE=BN,DE=DN.
(1)将两个矩形叠合成如图10,求证:四边形ABCD是菱形;
(2)若菱形ABCD的周长为20,BE=3,求矩形BEDG的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,点E、F、G、H分别在AB、BC、CD、AD边上且AE=CG,AH=CF.
(1)求证:四边形EFGH是平行四边形;
(2)如果AB=AD,且AH=AE,求证:四边形EFGH是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
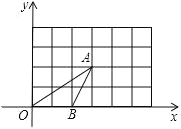
【题目】如图,△OAB的顶点坐标分别为O(0,0)、A(3,2)、B(2,0),将这三个顶点的坐标同时扩大到原来的2倍,得到对应点D、E、F.
(1)在图中画出△DEF;
(2)点E是否在直线OA上?为什么?
(3)△OAB与△DEF______位似图形(填“是”或“不是”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com