
【题目】如图,△ABC中AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cosA的值为( ) 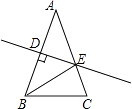
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:∵△ABC中,AB=AC=4,∠C=72°, ∴∠ABC=∠C=72°,∠A=36°,
∵D是AB中点,DE⊥AB,
∴AE=BE,
∴∠ABE=∠A=36°,
∴∠EBC=∠ABC﹣∠ABE=36°,
∠BEC=180°﹣∠EBC﹣∠C=72°,
∴∠BEC=∠C=72°,
∴BE=BC,
∴AE=BE=BC.
设AE=x,则BE=BC=x,EC=4﹣x.
在△BCE与△ABC中,![]() ,
,
∴△BCE∽△ABC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得x=﹣2±2 ![]() (负值舍去),
(负值舍去),
∴AE=﹣2+2 ![]() .
.
在△ADE中,∵∠ADE=90°,
∴cosA= ![]() =
= ![]() =
= ![]() .
.
故选C.
【考点精析】通过灵活运用解直角三角形,掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)即可以解答此题.


 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】公元前5世纪,毕达哥拉斯学派中的一名成员希伯索斯发现了无理数![]() ,导致了第一次数学危机.
,导致了第一次数学危机.![]() 是无理数的证明如下:
是无理数的证明如下:
假设![]() 是有理数,那么它可以表示成
是有理数,那么它可以表示成![]() (
(![]() 与
与![]() 是互质的两个正整数).于是
是互质的两个正整数).于是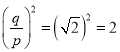 ,所以,
,所以,![]() .于是
.于是![]() 是偶数,进而
是偶数,进而![]() 是偶数.从而可设
是偶数.从而可设![]() ,所以
,所以![]() ,
,![]() ,于是可得
,于是可得![]() 也是偶数.这与“
也是偶数.这与“![]() 与
与![]() 是互质的两个正整数”矛盾,从而可知“
是互质的两个正整数”矛盾,从而可知“![]() 是有理数”的假设不成立,所以,
是有理数”的假设不成立,所以,![]() 是无理数.这种证明“
是无理数.这种证明“![]() 是无理数”的方法是( )
是无理数”的方法是( )
A.综合法B.反证法C.举反例法D.数学归纳法
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天水某公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两行环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元,
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1220万元,且确保这10辆公交车在该线路的年均载客量总和不少于650万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界读书日,某书店举办“书香”图书展,已知《汉语成语大词典》和《中华上 下五千年》两本书的标价总和为![]() 元,《汉语成语大词典》按标价的
元,《汉语成语大词典》按标价的![]() 折出售,《中华 上下五千年》按标价的
折出售,《中华 上下五千年》按标价的![]() 折出售,小明花
折出售,小明花![]() 元买了这两本书,求这两本书的标价各多少元?
元买了这两本书,求这两本书的标价各多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A(2,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(a,b),且a=![]() +
+![]() -6
-6
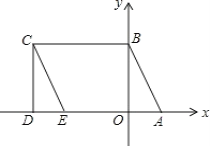
(1)求点C的坐标;
(2)求点E的坐标;
(3)点P是CE上一动点,设∠CBP=x°,∠PAD=y°,∠BPA=z°,确定x,y,z之间的数量c关系,并证明你的结论
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC向右平移3个单位长度,再向上平移2个单位长度,可以得到![]() .
.

(1)画出平移后的![]() ;
;
(2)写出![]() 三个顶点的坐标;
三个顶点的坐标;
(3)已知点P在x轴上,以![]() 、
、![]() 、P为顶点的三角形面积为4,求点P的坐标.
、P为顶点的三角形面积为4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
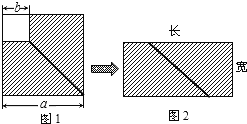
【题目】如图,边长为![]() 的大正方形内有一个边长为
的大正方形内有一个边长为![]() 的小正方形.
的小正方形.
(1)用含字母的代数式表示图1中阴影都分的面积为______________;
(2)图1的阴影部分沿斜线剪开局,拼成了一个如图2所示的长方形,用含字母的代数式表示此长方形的面积为_____________(多项式乘积的形式);
(3)比较左、右两图的阴影都分面积,请你写出一个整式乘法的公式_____________;
(4)结合(3)的公式,计算:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com