
【题目】在四边形![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在线段
在线段![]() 上运动.
上运动.
(1)如图1,已知![]() .
.

①若![]() 平分
平分![]() ,则
,则![]() ______;
______;
②若![]() ,试说明
,试说明![]() ;
;
(2)如图2,已知![]() ,试说明
,试说明![]() 平分
平分![]() .
.

【答案】(1)①90°;②证明见解析;(2)证明见解析.
【解析】
(1)①由![]() 可得
可得![]() ,根据平行线的性质可得∠ABC+∠BCD=180°,已知BF平分∠ABC,CE平分∠BCD,由角平分线的定义可得∠FBC=
,根据平行线的性质可得∠ABC+∠BCD=180°,已知BF平分∠ABC,CE平分∠BCD,由角平分线的定义可得∠FBC=![]() ∠ABC,∠BCF=
∠ABC,∠BCF=![]() ∠BCD,所以∠FBC+∠BCF=
∠BCD,所以∠FBC+∠BCF=![]() ∠ABC+
∠ABC+![]() ∠BCD=
∠BCD=![]() (∠ABC+∠BCD)=
(∠ABC+∠BCD)=![]() ×180°=90°,即可得∠BFC=90°;②已知CE平分∠BCD,由角平分线的定义可得∠DCE=∠BCF,根据等角的余角相等可得∠FBC=∠DEC;再利用同角的补角相等证得∠ABF=∠DEC,所以∠DEC=∠ABF=∠FBC,即可得
×180°=90°,即可得∠BFC=90°;②已知CE平分∠BCD,由角平分线的定义可得∠DCE=∠BCF,根据等角的余角相等可得∠FBC=∠DEC;再利用同角的补角相等证得∠ABF=∠DEC,所以∠DEC=∠ABF=∠FBC,即可得![]() ;(2)已知CE平分∠BCD,由角平分线的性质可得∠DCE=∠BCF,由三角形的内角和定理可证得∠FBC=∠DEC;由∠BFC+∠BFE=180°,∠BFC=∠A,可得∠BFE+∠A=180°,再由四边形的内角和为360°可得∠ABF+∠AEF=180°,再利用同角的补角相等证得∠ABF=∠DEC,所以∠DEC=∠ABF=∠FBC,即可得
;(2)已知CE平分∠BCD,由角平分线的性质可得∠DCE=∠BCF,由三角形的内角和定理可证得∠FBC=∠DEC;由∠BFC+∠BFE=180°,∠BFC=∠A,可得∠BFE+∠A=180°,再由四边形的内角和为360°可得∠ABF+∠AEF=180°,再利用同角的补角相等证得∠ABF=∠DEC,所以∠DEC=∠ABF=∠FBC,即可得![]() .
.
(1)∵![]() ,
,
∴![]() ,
,
∴∠ABC+∠BCD=180°,
∵BF平分∠ABC,CE平分∠BCD,
∴∠FBC=![]() ∠ABC,∠BCF=
∠ABC,∠BCF=![]() ∠BCD,
∠BCD,
∴∠FBC+∠BCF=![]() ∠ABC+
∠ABC+![]() ∠BCD=
∠BCD=![]() (∠ABC+∠BCD)=
(∠ABC+∠BCD)=![]() ×180°=90°,
×180°=90°,
∴∠BFC=90°;
故答案为:90°;
②∵CE平分∠BCD,
∴∠DCE=∠BCF,
∵∠BFC=∠D=90°,
∴∠BCF+∠FBC=90°,∠DEC+∠ECD=90°,
∴∠FBC=∠DEC;
∵∠ABF+∠AEF=180°,∠DEC+∠AEF=180°,
∴∠ABF=∠DEC,
∴∠DEC=∠ABF=∠FBC,
∴![]() ;
;
(2)∵CE平分∠BCD,
∴∠DCE=∠BCF,
∵∠BFC=∠D,
∴∠FBC=∠DEC;
∵∠BFC+∠BFE=180°,∠BFC=∠A,
∴∠BFE+∠A=180°,
∴∠ABF+∠AEF=180°,
∵∠DEC+∠AEF=180°,
∴∠ABF=∠DEC,
∴∠DEC=∠ABF=∠FBC,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】校园内有一个花坛,是由两个边长均为2.5m的正六边形围成的(如图中的阴影部分所示),学校现要将这个花坛在原有的基础上扩建成一个如图所示的菱形区域,则扩建后菱形区域的周长为( )

A.30mB.![]() mC.20mD.
mC.20mD.![]() m
m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
二次根式的除法,要化去分母中的根号,需将分子、分母同乘以一个恰当的二次根式.
例如:化简![]() .
.
解:将分子、分母同乘以![]() 得:
得:![]() .
.
类比应用:
(1)化简:![]() ;
;
(2)化简:![]() .
.
拓展延伸:
宽与长的比是![]() 的矩形叫黄金矩形.如图①,已知黄金矩形ABCD的宽AB=1.
的矩形叫黄金矩形.如图①,已知黄金矩形ABCD的宽AB=1.
(1)黄金矩形ABCD的长BC= ;
(2)如图②,将图①中的黄金矩形裁剪掉一个以AB为边的正方形ABEF,得到新的矩形DCEF,猜想矩形DCEF是否为黄金矩形,并证明你的结论;

(3)在图②中,连结AE,则点D到线段AE的距离为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的方程![]() ,
,
(1)求证:无论k取任何实数值,方程总有实数根;
(2)若等腰三角形ABC的一边长a=1,两个边长b,c恰好是这个方程的两个根,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
(参考数据:sin48°≈ ![]() ,tan48°≈
,tan48°≈ ![]() ,sin64°≈
,sin64°≈ ![]() ,tan64°≈2)
,tan64°≈2)
查看答案和解析>>
科目:初中数学 来源: 题型:
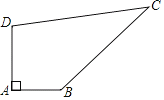
【题目】如图,某开发区有一块四边形的空地ABCD,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,则要投入_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com