
����Ŀ����֪������ABCD�У�AB=4cm��BC=8cm��AC�Ĵ�ֱƽ����EF�ֱ�AD��BC�ڵ�E��F������ΪO��
��1����ͼ1������AF��CE����֤�ı���AFCEΪ���Σ�����AF�ij���
��2����ͼ2������P��Q�ֱ��A��C����ͬʱ����������AFB����CDE���������˶�һ�ܣ�����P��A��F��B��Aֹͣ����Q��C��D��E��Cֹͣ�����˶������У�
����֪��P���ٶ�Ϊÿ��5cm����Q���ٶ�Ϊÿ��4cm���˶�ʱ��Ϊt�룬��A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ����t��ֵ��
������P��Q���˶�·�̷ֱ�Ϊa��b����λ��cm��ab��0������֪A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ���a��b�����������ϵʽ��

���𰸡���1��֤����������AF=5cm��
��2������A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ��![]() �룮
�룮
��a��b�����������ϵʽ��a+b=12��ab��0����
��������
��1����֤���ı���AFCEΪƽ���ı��Σ��ٸ��ݶԽ����ഹֱƽ�ֵ�ƽ���ı��������������ж������ݹ��ɶ����������AF�ij���
��2����������ۿ�֪����P����BF�ϡ�Q����ED��ʱ�����ܹ���ƽ���ı��Σ�����ƽ���ı��ε������г�������⼴��.
��1��֤�������ı���ABCD�Ǿ��Σ�
��AD��BC��
���CAD=��ACB����AEF=��CFE��
��EF��ֱƽ��AC������ΪO��
��OA=OC��
���AOE�ա�COF��
��OE=OF��
���ı���AFCEΪƽ���ı��Σ�
�֡�EF��AC��
���ı���AFCEΪ���Σ�
�����εı߳�AF=CF=xcm����BF=��8��x��cm��
��Rt��ABF��AB=4cm��
�ɹ��ɶ�����42+��8��x��2=x2��
���x=5��
��AF=5cm��
��2������Ȼ��P����AF��ʱ��Q����CD�ϣ���ʱA��C��P��Q�ĵ㲻���ܹ���ƽ���ı��Σ�

ͬ��P����AB��ʱ��Q����DE��CE�ϣ�Ҳ���ܹ���ƽ���ı��Σ�
���ֻ�е�P����BF�ϡ�Q����ED��ʱ�����ܹ���ƽ���ı��Σ�
����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ��PC=QA��
�ߵ�P���ٶ�Ϊÿ��5cm����Q���ٶ�Ϊÿ��4cm���˶�ʱ��Ϊt�룬
��PC=5t��QA=12��4t��
��5t=12��4t��
���![]() ��
��
����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ��![]() �룮
�룮
��������ã���A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ����P��Q�ڻ���ƽ�еĶ�Ӧ���ϣ�
�����������
i����ͼ1����P����AF�ϡ�Q����CE��ʱ��AP=CQ����a=12��b����a+b=12��
ii����ͼ2����P����BF�ϡ�Q����DE��ʱ��AQ=CP����12��b=a����a+b=12��
iii����ͼ3����P����AB�ϡ�Q����CD��ʱ��AP=CQ����12��a=b����a+b=12��
����������a��b�����������ϵʽ��a+b=12��ab��0����



 �㽭֮��ѧҵˮƽ����ϵ�д�
�㽭֮��ѧҵˮƽ����ϵ�д� ��Ч���ܿ�ʱ��ҵϵ�д�
��Ч���ܿ�ʱ��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ı���![]() �У�
�У�![]() ƽ��
ƽ��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ���߶�
���߶�![]() ���˶�.
���˶�.
��1����ͼ1����֪![]() .
.

����![]() ƽ��
ƽ��![]() ����
����![]() ______��
______��
����![]() ����˵��
����˵��![]() ��
��
��2����ͼ2����֪![]() ����˵��
����˵��![]() ƽ��
ƽ��![]() .
.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijɽ����23���С�Сѧ����ƶ��ʧѧ��Ҫ����������һ����ѧ����ѧϰ������ҪaԪ��һ��Сѧ����ѧϰ������ҪbԪ��ijУѧ����������У����ѧ��ÿ���꼶���Էֱ������ƶ����ѧ����Сѧ��������������±���

��1����a,b��ֵ.
��2�����꼶ѧ���ľ����������ƶ����Сѧ����ѧϰ���ã�����꼶ѧ���ɾ�����ƶ�����С�Сѧ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �У�
�� ![]() ��
��![]() ��
��![]() ��
��![]() ����ƽ��5����λ����ƽ��4����λ֮��õ���ͼ��
����ƽ��5����λ����ƽ��4����λ֮��õ���ͼ��

��1��![]() ���������ֱ�Ϊ
���������ֱ�Ϊ![]()
![]() .
.
��2������![]() ƽ��֮���ͼ��
ƽ��֮���ͼ��![]() .
.
��3�����ABC�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���֪P��1��1��.����P�ֱ���x���y�������ߣ�����ֱ�ΪA��B.
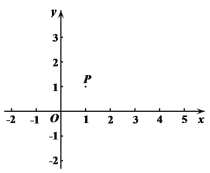
��1����Q��ֱ��AP�������P �ľ���Ϊ2�����Q������Ϊ ��������BPQ�������______��
��2��ƽ��������ABP��������Pƽ�ƺ�Ķ�Ӧ��Ϊ![]() ��4��3����
��4��3����
�ٻ���ƽ�ƺ��������![]() ��
��
��ֱ��д���ı���![]() �����Ϊ .
�����Ϊ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() �ӵ�
�ӵ�![]() ������
������![]() ������ÿ��2����λ���ȵ��ٶ����
������ÿ��2����λ���ȵ��ٶ����![]() �˶���ͬʱ��
�˶���ͬʱ��![]() �ӵ�
�ӵ�![]() ������
������![]() ������ÿ��1����λ���ȵ��ٶ����
������ÿ��1����λ���ȵ��ٶ����![]() �˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������
�˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������![]() ��
��![]() �˶���ʱ����
�˶���ʱ����![]() ��(
��(![]() )������
)������![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ��
��

��1����![]() ��
��![]() �ij���
�ij���
��2����֤��![]() ��
��
��3���ı���![]() �ܹ���Ϊ����������ܣ������Ӧ��
�ܹ���Ϊ����������ܣ������Ӧ��![]() ֵ��������ܣ�˵�����ɣ�
ֵ��������ܣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У���OΪ�Խ���AC���е㣬��O�������OM��ON�ֱ�AB��BC�ڵ�E��F���ҡ�EOF=90����BO��EF���ڵ�P����������ۣ�
��ͼ����ȫ�ȵ�������ֻ�����ԣ��ڡ�EOF�ǵ���ֱ�������Σ���������ABCD����������ı���OEBF�����4������BE��BF=![]() OA��
OA��
������ȷ���۵ĸ�����(����)

A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һλС�����ڲ���ƽ�����Ϲ���һ���뾶Ϊ5cm��Բ����������������BC��ʼ����ʱֹͣ����AB=40cm��BC��ˮƽ��ļн�Ϊ60�㣮��Բ����������·�߳���cm������������ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��M ���������IJ��̨�������� M ���������� 240km �� P ������ÿСʱ 45km ���ٶ�����ƫ�� 30���� PB �����ƶ�����̨������ 150km �ķ�Χ������̨��Ӱ��������� M �� ��̨��Ӱ���ʱ��Ϊ�� ��Сʱ��
A.4B.5C.6D.7
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com