
【题目】一位小朋友在不打滑的平面轨道上滚动一个半径为5cm的圆环,当滚到与坡面BC开始相切时停止.其AB=40cm,BC与水平面的夹角为60°.其圆心所经过的路线长是cm(结果保留根号).
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
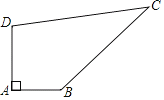
【题目】如图,某开发区有一块四边形的空地ABCD,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,则要投入_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
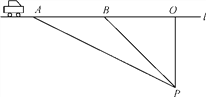
【题目】超速行驶是引发交通事故的主要原因.上周末,小鹏等三位同学在滨海大道红树林路段,尝试用自己所学的知识检测车速,观测点设在到公路l的距离为100米的P处.这时,一辆富康轿车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,试判断此车是否超过了每小时80千米的限制速度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,已知AD=10cm , 小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为( )
A.20cm
B.15cm
C.10cm
D.随直线MN的变化而变化
查看答案和解析>>
科目:初中数学 来源: 题型:
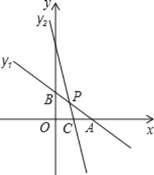
【题目】如图,在平面直角坐标系xOy中,一次函数y1=![]() x+2与x轴、y轴分别相交于点A和点B,直线y2=kx+b(k≠0)经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.
x+2与x轴、y轴分别相交于点A和点B,直线y2=kx+b(k≠0)经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.
(1)求A、B的坐标;
(2)求△ABO的面积;
(3)若△ABO被直线CP分成的两部分的面积相等,求点P的坐标及直线CP的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y= -![]() +1与x轴、y轴分别交于点A、点B(O为坐标原点),将△ABO绕着点B逆时针旋转60°后,点A恰好落在点C处,那么点C的坐标为___________
+1与x轴、y轴分别交于点A、点B(O为坐标原点),将△ABO绕着点B逆时针旋转60°后,点A恰好落在点C处,那么点C的坐标为___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线过点A(2,0),B(﹣1,0),与y轴交于点C,且OC=2.则这条抛物线的解析式为( )
A.y=x2﹣x﹣2
B.y=﹣x2+x+2
C.y=x2﹣x﹣2或y=﹣x2+x+2
D.y=﹣x2﹣x﹣2或y=x2+x+2
查看答案和解析>>
科目:初中数学 来源: 题型:
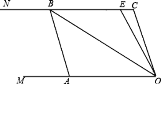
【题目】如图,已知两条射线OM∥CN,动线段AB的两个端点A,B分别在射线OM,CN上,且∠C=∠OAB=108°,点E在线段CB上,OB平分∠AOE.
(1)图中有哪些与∠AOC相等的角?并说明理由;
(2)若平移AB,那么∠OBC与∠OEC的度数比是否随着AB位置变化而变化?若变化,找出变化规律;若不变,求出这个比值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com