
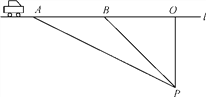
【题目】超速行驶是引发交通事故的主要原因.上周末,小鹏等三位同学在滨海大道红树林路段,尝试用自己所学的知识检测车速,观测点设在到公路l的距离为100米的P处.这时,一辆富康轿车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,试判断此车是否超过了每小时80千米的限制速度?
【答案】此车超过每小时80千米的限制速度.
【解析】试题分析: 首先,根据在直角三角形BPO中,∠BPO=45°,可得到BO=PO=100m,再根据在直角三角形APO中,∠APO=60°,运用三角函数值,可得到AO=100![]() ,根据AB=AO-BO可求得AB的长;再结合速度的计算方法,求出车的速度,然后将车的速度与80千米/时进行比较,即可得到结论.
,根据AB=AO-BO可求得AB的长;再结合速度的计算方法,求出车的速度,然后将车的速度与80千米/时进行比较,即可得到结论.
试题解析:
解:在Rt△APO中,∠APO=60°,则∠PAO=30°.
∴AP=2OP=200 m,
AO=![]() =
=![]() =100
=100![]() (m).
(m).
在Rt△BOP中,∠BPO=45°,
则BO=OP=100 m.
∴AB=AO-BO=100![]() -100≈73(m).
-100≈73(m).
∴从A到B小车行驶的速度为73÷3≈24.3(m/s)=87.48 km/h>80 km/h.
∴此车超过每小时80千米的限制速度.


科目:初中数学 来源: 题型:
【题目】如图,已知EF⊥BC,AD⊥BC, ∠1=∠2,
⑴判断DM与AB的位置关系,并说明理由;
⑵若∠BAC=70°,DM平分∠ADC,求∠ACB的度数。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中, ![]() ,
,![]() ;
;![]() 是
是![]() 向右平移5个单位向上平移4个单位之后得到的图象
向右平移5个单位向上平移4个单位之后得到的图象

(1)![]() 两点的坐标分别为
两点的坐标分别为![]()
![]() .
.
(2)作出![]() 平移之后的图形
平移之后的图形![]() .
.
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒2个单位长度的速度向点
方向以每秒2个单位长度的速度向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒1个单位长度的速度向点
方向以每秒1个单位长度的速度向点![]() 运动,当其中一个点到达终点时,另一个点也随之停止运动,设点
运动,当其中一个点到达终点时,另一个点也随之停止运动,设点![]() ,
,![]() 运动的时间是
运动的时间是![]() 秒(
秒(![]() ).过点
).过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.

(1)求![]() 、
、![]() 的长;
的长;
(2)求证:![]() ;
;
(3)四边形![]() 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的![]() 值;如果不能,说明理由.
值;如果不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点O为对角线AC的中点,过O点的射线OM,ON分别交AB,BC于点E,F,且∠EOF=90°,BO,EF交于点P,则下面结论:
①图形中全等的三角形只有三对;②△EOF是等腰直角三角形;③正方形ABCD的面积等于四边形OEBF面积的4倍;④BE+BF=![]() OA.
OA.
其中正确结论的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线BC//ED.
(1)如图1,若点A在直线DE上,且∠B=44°,∠EAC=57°,求∠BAC的度数;
(2)如图2,若点A是直线DE的上方一点,点G在BC的延长线上求证:∠ACG=∠BAC+∠ABC;
(3)如图3,FH平分∠AFE,CH平分∠ACG,且∠FHC比∠A的2倍少60°,直接写出∠A的度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位小朋友在不打滑的平面轨道上滚动一个半径为5cm的圆环,当滚到与坡面BC开始相切时停止.其AB=40cm,BC与水平面的夹角为60°.其圆心所经过的路线长是cm(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
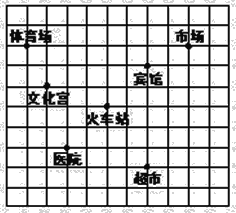
【题目】如图,这是某市部分简图,为了确定各建筑物的位置:
(1)请你以火车站为原点建立平面直角坐标系﹒
(2)写出超市的坐标(小正方形网格的单位长度为1)﹒
(3)请将体育场、宾馆和火车站看作三点,用线段连接起来,得到三角形ABC,然后将此三角形向下平移4个单位,再画出平移后的三角形A′B′C′,并计算三角形A′B′C′的面积﹒
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com