
【题目】如图,已知EF⊥BC,AD⊥BC, ∠1=∠2,
⑴判断DM与AB的位置关系,并说明理由;
⑵若∠BAC=70°,DM平分∠ADC,求∠ACB的度数。

科目:初中数学 来源: 题型:
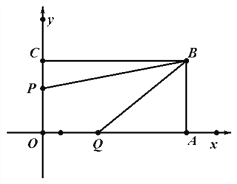
【题目】如图长方形OABC的位置如图所示,点B的坐标为(8,4),点P从点C出发向点O移动,速度为每秒1个单位;点Q同时从点O出发向点A移动,速度为每秒2个单位,设运动时间为t(0≤t≤4)
(1)填空:点A的坐标为 ,点C的坐标为 ,点P的坐标为 (用含t的代数式表示)
(2)当t为何值时,P、Q两点与原点距离相等?
(3)在点P、Q移动过程中,四边形OPBQ的面积是否变化?说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
二次根式的除法,要化去分母中的根号,需将分子、分母同乘以一个恰当的二次根式.
例如:化简![]() .
.
解:将分子、分母同乘以![]() 得:
得:![]() .
.
类比应用:
(1)化简:![]() ;
;
(2)化简:![]() .
.
拓展延伸:
宽与长的比是![]() 的矩形叫黄金矩形.如图①,已知黄金矩形ABCD的宽AB=1.
的矩形叫黄金矩形.如图①,已知黄金矩形ABCD的宽AB=1.
(1)黄金矩形ABCD的长BC= ;
(2)如图②,将图①中的黄金矩形裁剪掉一个以AB为边的正方形ABEF,得到新的矩形DCEF,猜想矩形DCEF是否为黄金矩形,并证明你的结论;

(3)在图②中,连结AE,则点D到线段AE的距离为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
(参考数据:sin48°≈ ![]() ,tan48°≈
,tan48°≈ ![]() ,sin64°≈
,sin64°≈ ![]() ,tan64°≈2)
,tan64°≈2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量出楼房AC的高度,从距离楼底C处60 ![]() 米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:
米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1: ![]() 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈ ![]() ,计算结果用根号表示,不取近似值).
,计算结果用根号表示,不取近似值).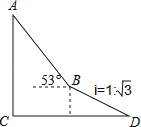
查看答案和解析>>
科目:初中数学 来源: 题型:
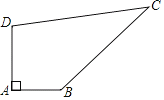
【题目】如图,某开发区有一块四边形的空地ABCD,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,则要投入_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD,把△BCD沿BD翻折,得△BDG,BG,AD所在的直线交于点E,过点D作DF∥BE交BC所在直线于点F.

(1)求证:四边形DEBF是菱形;
(2)若AB=8,AD=4,求四边形BEDF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
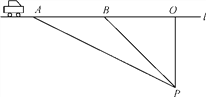
【题目】超速行驶是引发交通事故的主要原因.上周末,小鹏等三位同学在滨海大道红树林路段,尝试用自己所学的知识检测车速,观测点设在到公路l的距离为100米的P处.这时,一辆富康轿车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,试判断此车是否超过了每小时80千米的限制速度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com