
【题目】已知矩形ABCD,把△BCD沿BD翻折,得△BDG,BG,AD所在的直线交于点E,过点D作DF∥BE交BC所在直线于点F.

(1)求证:四边形DEBF是菱形;
(2)若AB=8,AD=4,求四边形BEDF的面积.
【答案】(1)详见解析;(2)80
【解析】
(1)首先根据矩形性质得出AD∥BC,从而得出∠EDB=∠DBC,然后结合折叠性质可知∠DBG=∠DBC,据此进一步证明出DE=BE,最后通过证明四边形BEDF为平行四边形进一步证明其是菱形即可;
(2)设菱形BEDF的边长为![]() ,则AE=DEAD=
,则AE=DEAD=![]() ,根据勾股定理求出
,根据勾股定理求出![]() 的值,然后进一步加以计算即可.
的值,然后进一步加以计算即可.
(1)证明:
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠EDB=∠DBC,
根据折叠性质可知:∠DBG=∠DBC,
∴∠EDB=∠EBD,
∴DE=BE,
∵AD∥BC,DF∥BE,
∴四边形BEDF为平行四边形,
又∵DE=BE,
∴四边形BEDF为菱形;
(2)设菱形BEDF的边长为![]() ,则AE=DEAD=
,则AE=DEAD=![]() ,
,
在Rt△AEB中,![]() ,
,
即:![]()
解得:![]() ,
,
∴菱形BEDF的面积=DE×AB=10×8=80.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知四边形ABCD,其中AD//BC,AB⊥BC,将DC沿DE折叠,C落于![]() ,
,![]() 交CB于G,且ABGD为长方形(如图1);再将纸片展开,将AD沿DF折叠,使A点落在DC上一点
交CB于G,且ABGD为长方形(如图1);再将纸片展开,将AD沿DF折叠,使A点落在DC上一点![]() (如图2),在两次折叠过程中,两条折痕DE、DF所成的角为____________度.
(如图2),在两次折叠过程中,两条折痕DE、DF所成的角为____________度.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知EF⊥BC,AD⊥BC, ∠1=∠2,
⑴判断DM与AB的位置关系,并说明理由;
⑵若∠BAC=70°,DM平分∠ADC,求∠ACB的度数。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.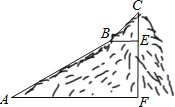
(1)求AB段山坡的高度EF;
(2)求山峰的高度CF.( ![]() 1.414,CF结果精确到米)
1.414,CF结果精确到米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某山区有23名中、小学生因贫困失学需要捐助,资助一名中学生的学习费用需要a元,一名小学生的学习费用需要b元,某校学生积极捐款,我校初中学生每个年级各自分别捐助的贫困中学生和小学生的人数情况如下表:

(1)求a,b的值.
(2)九年级学生的捐款解决了其余贫困中小学生的学习费用,求九年级学生可捐助的贫困生中、小学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了改善小区环境,某小区决定要在一块一边靠墙(墙长 25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为 40m 的栅栏围住(如图).设绿化带的BC 边长为x m,绿化带的面积为y m2 . 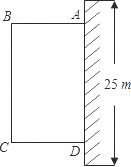
(1)求y 与x 之间的函数关系式,并写出自变量x 的取值范围.
(2)当x 为何值时,满足条件的绿化带的面积最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中, ![]() ,
,![]() ;
;![]() 是
是![]() 向右平移5个单位向上平移4个单位之后得到的图象
向右平移5个单位向上平移4个单位之后得到的图象

(1)![]() 两点的坐标分别为
两点的坐标分别为![]()
![]() .
.
(2)作出![]() 平移之后的图形
平移之后的图形![]() .
.
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒2个单位长度的速度向点
方向以每秒2个单位长度的速度向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒1个单位长度的速度向点
方向以每秒1个单位长度的速度向点![]() 运动,当其中一个点到达终点时,另一个点也随之停止运动,设点
运动,当其中一个点到达终点时,另一个点也随之停止运动,设点![]() ,
,![]() 运动的时间是
运动的时间是![]() 秒(
秒(![]() ).过点
).过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.

(1)求![]() 、
、![]() 的长;
的长;
(2)求证:![]() ;
;
(3)四边形![]() 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的![]() 值;如果不能,说明理由.
值;如果不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
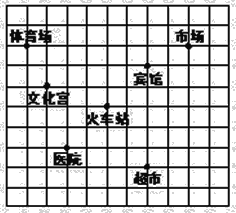
【题目】如图,这是某市部分简图,为了确定各建筑物的位置:
(1)请你以火车站为原点建立平面直角坐标系﹒
(2)写出超市的坐标(小正方形网格的单位长度为1)﹒
(3)请将体育场、宾馆和火车站看作三点,用线段连接起来,得到三角形ABC,然后将此三角形向下平移4个单位,再画出平移后的三角形A′B′C′,并计算三角形A′B′C′的面积﹒
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com