
【题目】如图,在矩形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 上一个动点,连接
上一个动点,连接![]() ,将
,将![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处,连接
处,连接![]() ,若
,若![]() 是直角三角形,则
是直角三角形,则![]() 的长为___________.
的长为___________.

【答案】![]() 或
或![]()
【解析】
由题意可知∠ECF≠90°,故分两种情况:①当∠EFC=90°时,②当∠CEF=90°时,分别利用折叠的性质和勾股定理求出BE,即可得到CE的长.
解:由题意可知∠ECF≠90°,故分两种情况:
①当∠EFC=90°时,如图1,
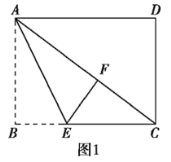
∵∠AFE=∠B=90°,∠EFC=90°,
∴A、F、C三点共线,
∵![]() ,
,
∴![]() ,
,
设BE=x,则EF=x,CE=4-x,
∵AF=AB=3,
∴FC=5-3=2,
在Rt△CEF中,EF2+FC2=CE2,
∴![]() ,
,
解得:![]() ,
,
∴CE=4-x=![]() ;
;
②当∠CEF=90°时,如图2,
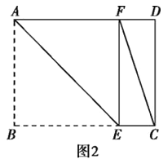
由折叠的性质得:∠AEB=∠AEF=![]() ,
,
∴AB=BE=3,
∴CE=4-3=1,
综上所述,![]() 的长为1或
的长为1或![]() ,
,
故答案为:1或![]() .
.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】如图所示,A(2,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(a,b),且a=![]() +
+![]() -6
-6
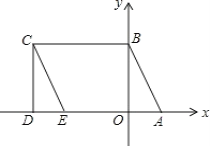
(1)求点C的坐标;
(2)求点E的坐标;
(3)点P是CE上一动点,设∠CBP=x°,∠PAD=y°,∠BPA=z°,确定x,y,z之间的数量c关系,并证明你的结论
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD,其中AD//BC,AB⊥BC,将DC沿DE折叠,C落于![]() ,
,![]() 交CB于G,且ABGD为长方形(如图1);再将纸片展开,将AD沿DF折叠,使A点落在DC上一点
交CB于G,且ABGD为长方形(如图1);再将纸片展开,将AD沿DF折叠,使A点落在DC上一点![]() (如图2),在两次折叠过程中,两条折痕DE、DF所成的角为____________度.
(如图2),在两次折叠过程中,两条折痕DE、DF所成的角为____________度.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 中,对角线
中,对角线![]() 和
和![]() 交于点
交于点![]() ,且点
,且点![]() 是
是![]() 和
和![]() 的中点,若
的中点,若![]() 的长为10,则
的长为10,则![]() 和
和![]() 的长可以是( )
的长可以是( )

A. 5和10B. 8和12C. 10和20D. 20和40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通常情况下,用两种不同的方法计算同一图形的面积,可以得到一个恒等式,
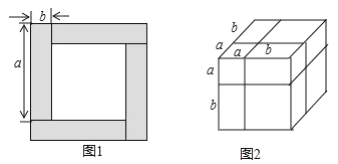
①如图1,根据图中阴影部分的面积可表示为__________,还可表示为___________,可以得到的恒等式是___________.
②类似地,用两种不同的方法计算同一各几何体的体积,也可以得到一个恒等式,如图2是边长为![]() 的正方体,被如图所示的分割线分成8块。用不同方法计算这个正方体的体积,就可以得到一个恒等式,这个恒等式是____________.
的正方体,被如图所示的分割线分成8块。用不同方法计算这个正方体的体积,就可以得到一个恒等式,这个恒等式是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知EF⊥BC,AD⊥BC, ∠1=∠2,
⑴判断DM与AB的位置关系,并说明理由;
⑵若∠BAC=70°,DM平分∠ADC,求∠ACB的度数。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.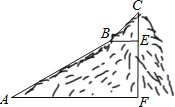
(1)求AB段山坡的高度EF;
(2)求山峰的高度CF.( ![]() 1.414,CF结果精确到米)
1.414,CF结果精确到米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒2个单位长度的速度向点
方向以每秒2个单位长度的速度向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒1个单位长度的速度向点
方向以每秒1个单位长度的速度向点![]() 运动,当其中一个点到达终点时,另一个点也随之停止运动,设点
运动,当其中一个点到达终点时,另一个点也随之停止运动,设点![]() ,
,![]() 运动的时间是
运动的时间是![]() 秒(
秒(![]() ).过点
).过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.

(1)求![]() 、
、![]() 的长;
的长;
(2)求证:![]() ;
;
(3)四边形![]() 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的![]() 值;如果不能,说明理由.
值;如果不能,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com