
【题目】如图,为了测量出楼房AC的高度,从距离楼底C处60 ![]() 米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:
米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1: ![]() 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈ ![]() ,计算结果用根号表示,不取近似值).
,计算结果用根号表示,不取近似值).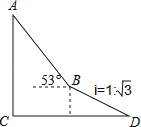
【答案】解:如图作BN⊥CD于N,BM⊥AC于M.
在RT△BDN中,BD=30,BN:ND=1: ![]() ,
,
∴BN=15,DN=15 ![]() ,
,
∵∠C=∠CMB=∠CNB=90°,
∴四边形CMBN是矩形,
∴CM=BM=15,BM=CN=60 ![]() ﹣15
﹣15 ![]() =45
=45 ![]() ,
,
在RT△ABM中,tan∠ABM= ![]() =
= ![]() ,
,
∴AM=27 ![]() ,
,
∴AC=AM+CM=15+27 ![]() .
.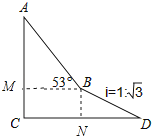
【解析】如图作BN⊥CD于N,BM⊥AC于M,先在RT△BDN中求出线段BN,在RT△ABM中求出AM,再证明四边形CMBN是矩形,得CM=BN即可解决问题.本题考查解直角三角形、仰角、坡度等概念,解题的关键是添加辅助线构造直角三角形,记住坡度的定义,属于中考常考题型.
【考点精析】本题主要考查了关于坡度坡角问题和关于仰角俯角问题的相关知识点,需要掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA;仰角:视线在水平线上方的角;俯角:视线在水平线下方的角才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 中,对角线
中,对角线![]() 和
和![]() 交于点
交于点![]() ,且点
,且点![]() 是
是![]() 和
和![]() 的中点,若
的中点,若![]() 的长为10,则
的长为10,则![]() 和
和![]() 的长可以是( )
的长可以是( )

A. 5和10B. 8和12C. 10和20D. 20和40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通常情况下,用两种不同的方法计算同一图形的面积,可以得到一个恒等式,
①如图1,根据图中阴影部分的面积可表示为__________,还可表示为___________,可以得到的恒等式是___________.
②类似地,用两种不同的方法计算同一各几何体的体积,也可以得到一个恒等式,如图2是边长为![]() 的正方体,被如图所示的分割线分成8块。用不同方法计算这个正方体的体积,就可以得到一个恒等式,这个恒等式是____________.
的正方体,被如图所示的分割线分成8块。用不同方法计算这个正方体的体积,就可以得到一个恒等式,这个恒等式是____________.
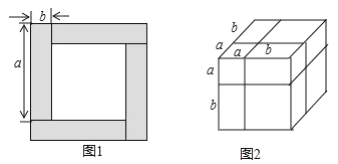
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知EF⊥BC,AD⊥BC, ∠1=∠2,
⑴判断DM与AB的位置关系,并说明理由;
⑵若∠BAC=70°,DM平分∠ADC,求∠ACB的度数。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有A、B、C三种不同型号的卡片,每种卡片各有9张.其中A型卡片是边长为3的正方形,B型卡片是相邻两边长分别为3、1的长方形,C型卡片是边长为1的正方形.从其中取若干张卡片(每种卡片至少取1张),若把取出的这些卡片拼成一个正方形,则所拼正方形的边长的最大值是______.
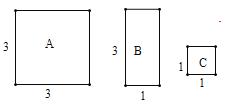
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.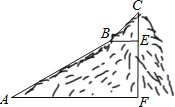
(1)求AB段山坡的高度EF;
(2)求山峰的高度CF.( ![]() 1.414,CF结果精确到米)
1.414,CF结果精确到米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了改善小区环境,某小区决定要在一块一边靠墙(墙长 25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为 40m 的栅栏围住(如图).设绿化带的BC 边长为x m,绿化带的面积为y m2 . 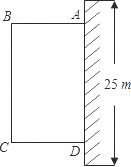
(1)求y 与x 之间的函数关系式,并写出自变量x 的取值范围.
(2)当x 为何值时,满足条件的绿化带的面积最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线BC//ED.
(1)如图1,若点A在直线DE上,且∠B=44°,∠EAC=57°,求∠BAC的度数;
(2)如图2,若点A是直线DE的上方一点,点G在BC的延长线上求证:∠ACG=∠BAC+∠ABC;
(3)如图3,FH平分∠AFE,CH平分∠ACG,且∠FHC比∠A的2倍少60°,直接写出∠A的度数.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com